Если любой эл. обратен самому-себе то группа-Абелева. Док-во

[cxzbsdhwert]

mihaild в сообщении #1714683 писал(а):

чему равно $a \cdot b$?

1) $b$, если $a=e$; 2) $e$, если $b=e$; 3) $a$ или $b$ во всех остальных случаях, так чтобы для них также выполнялась ассоциативность (это вроде не зависит от описания, то есть при соблюдении описания остальные наборы как могут быть ассоциативны, так могут и не быть).

[mihaild]

cxzbsdhwert в сообщении #1714689 писал(а):

1) $b$, если $a=e$;

У меня уже три отдельных элемента, $a \neq e$.

cxzbsdhwert в сообщении #1714689 писал(а):

$a$ или $b$ во всех остальных случаях, так чтобы для них также выполнялась ассоциативность

А вдруг не получится?

Нельзя просто так взять и сказать "ну возьмем какой-нибудь объект с нужными свойствами", когда требуется доказать существование такого объекта.

[cxzbsdhwert]

mihaild в сообщении #1714688 писал(а):

Раз нельзя привести - то не является. Потому что пример - это пример, конкретная полугруппа. А у вас какие-то условия на полугруппу, которые не факт что вообще бывают выполнены все вместе.

Нет, нельзя привести в том смысле, что если Вы приводите операцию, которая удовлетворяет описанию, но не уточняете какая это именно операция (поскольку их множество), то точно утверждать нельзя, можно только угадывать.

mihaild в сообщении #1714688 писал(а):

А почему такая операция вообще существует? Так задача у Вас - доказать, что такая полугруппа существует. А Вы от меня её просите. А вдруг такой не бывает?

Ну так работает доказательство от противного (только прокаченное).
Утверждение: "есть полугруппа у которой есть левый нейтральный но нет правого". От обратного - "пускай если есть левый нейтральный, то он всегда нейтральный и справа".
Я привёл пример когда нейтральный левый, справа оказался не нейтральным - противоречие.
Только я привёл не один конкретный пример, а как-бы класс, которому удовлетворяет множество конкретных примеров. Если Вы хотите конкретный, пожалуйста (это не определитель, а таблица всех значений операции):

$(\{a,b,e\},\circ), \circ(x,y)=\begin{bmatrix} _{x/y}&a &b &e \\ a&a &b &e \\ b&a &b &e \\ e&a &b &e \end{bmatrix}$

Пример, который я привёл выше сводится к более универсальному выражению $(x,y)\rightarrow y$. Возможно это единственный вариант, когда есть левый но нет правого нейтрального.

Кстати, ещё наблюдение: здесь походу больше одного нейтрального. Ну, видимо все - нейтральные. Интересно.

Но при этом тут вроде нет обратного. Могу предположить, что введение обратного немедленно приводит к "схлопыванию" нейтральных в один, и те которые были нейтральными, и теперь ими перестают быть, становятся обратными по отношению к кому-то.

[mihaild]

cxzbsdhwert в сообщении #1714692 писал(а):

Нет, нельзя привести в том смысле, что если Вы приводите операцию, которая удовлетворяет описанию, но не уточняете какая это именно операция (поскольку их множество), то точно утверждать нельзя, можно только угадывать.

Так это Ваша задача - привести операцию. Ну либо показать, что все операции с какими-то свойствами подходят, и доказать, что хотя бы одна операция с этими свойствами существует.

cxzbsdhwert в сообщении #1714692 писал(а):

Я привёл пример когда нейтральный левый

Нет, Вы не привели пример. Пример - это конкретная группа, из него должно быть понятно, как перемножить любые два элемента.

cxzbsdhwert в сообщении #1714692 писал(а):

Пример, который я привёл выше сводится к более универсальному выражению $(x,y)\rightarrow y$.

Вот, это уже конкретный пример (вместе с указанием носителя). По нему я могу сказать, какое значение операции на любых аргументах. Еще надо бы доказать ассоциативность, но это тривиально.

cxzbsdhwert в сообщении #1714692 писал(а):

Возможно это единственный вариант, когда есть левый но нет правого нейтрального

Нет конечно, есть огромное количество и других операций с этим свойством (я не уверен, что их все можно как-то разумно описать).

cxzbsdhwert в сообщении #1714692 писал(а):

Могу предположить, что введение обратного немедленно приводит к "схлопыванию" нейтральных в один, и те которые были нейтральными, и теперь ими перестают быть, становятся обратными по отношению к кому-то.

А это уже вторая задача. Если в полугруппе существует левый нейтральный $e$, такой что $\forall a: ea = a$, и существует левый обратный: $\forall a \exists x: xa = e$, то это группа.

[cxzbsdhwert]

mihaild
А что, только левого нейтрального в полугруппе не достаточно для моноида получается? Но достаточно, правда вместе с левым обратным, для группы?

[mihaild]

cxzbsdhwert в сообщении #1714722 писал(а):

А что, только левого нейтрального в полугруппе не достаточно для моноида получается?

Да, Вы же нашли полугруппу с левым обратном, не являющуюся моноидом.

cxzbsdhwert в сообщении #1714722 писал(а):

Но достаточно, правда вместе с левым обратным, для группы?

А это как раз следующее упражнение.

[cxzbsdhwert]

mihaild в сообщении #1714734 писал(а):

Да, Вы же нашли полугруппу с левым обратном, не являющуюся моноидом

Ну это же насколько я понял, вопрос определения, вопрос аксиом как Вы сами ранее написали. То есть, может моноид по другому определяется как полугруппа с левым обратным, а правый может быть а может не быть, и тогда ведь определение группы сохраняется - моноид, с левым обратным. Тут хочется сразу сказать, что моноид без правого нейтрального тогда тоже, доопределив к нему левый обратный, должен быть группой, а такого быть не может. Но Вы же наверное не сможете предъявить моноид без правого нейтрального но при этом с обратным, и тогда противоречия нет.

[mihaild]

cxzbsdhwert в сообщении #1714743 писал(а):

Ну это же насколько я понял, вопрос определения, вопрос аксиом как Вы сами ранее написали

А вот тут именно тот момент, о котором выше писал F111mon. Есть несколько разных аксиоматизаций, но понятие группы, как и понятия моноида - одно. Все эти аксиоматизации эквивалентны - например классы "полугруппа с единицей и обратным" и "полугруппа с левой единицей и левым обратным" совпадают, поэтому группу можно определять и так и так.. Моноид, по определению - полугруппа с единицей. И, раз мы знаем, что полугруппы бывают с левой единицей, но без двусторонней, то определять моноид как полугруппу с левой единицей нельзя - это другой класс структур, более широкий.
Поэтому говорить "моноид без правого нейтрального" нельзя.
Можно спросить, что будет если в полугруппе есть левый нейтральный и двусторонний обратный. Но выше есть даже более сильное утверждение - полугруппа с левым нейтральным и левым (а не двусторонним) обратным - это группа.

[cxzbsdhwert]

mihaild F111mon
Ну вроде пришёл к доказательству. Текста много. Возможно рассуждения вокруг равенств $(*)$ лишние, как и сами равенства. Главные доказательства во второй половине.

(Оффтоп)

Я во-первых немного более осмысленно посмотрел на ранее приведённое тут техническое доказательство того, что если есть левый и правый то они совпадают. Ну получается что если левый и правый есть то они должны совпадать чтобы выполнялась ассоциативность. Если в полугруппе есть $b$, и у него левый обратный $a$ и правый $c$, то по ассоциативности: $(ab)c=c=a=a(bc)$

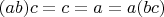
Пусть в полугруппе есть (единый) левый нейтральный $a$ и левый обратный для каждого. Таблица значений операции для конечного множества из четырёх элементов такова:

$$\circ(\text{левый}, \text{правый})=\begin{bmatrix} _{\frac{\text{правый}\to}{\text{левый}\downarrow}}&a &b &c &d\\ a&a &b &c &d\\ b& & & &\\ c& & & &\\ d& & & &\\ \end{bmatrix}$$

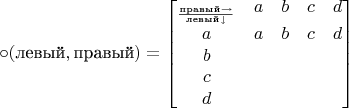
По условию левый обратный есть у каждого. Разберёмся с левыми обратными для $b,c,d$. Ими не может быть $a$, потому что пара с ним слева для $b,c,d$ уже определена. Значит обратными к $b,c,d$ могут быть только они сами.
Варианты могут быть такие:
1) симметричные левые обратные (если $a$ - левый обратный к $b$, то $b$ - левый обратный к $a$), и частный случай - 1.1) элемент обратен сам себе;
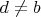
2) несимметричные левые обратные. $b$ - левый обратный к $c$, но $c$ левый обратный к $d\neq b$. Вообще-говоря на данном этапе это не значит, что $c$ - не левый обратный к $b$, поскольку это означало бы что у $c$ два правых обратных, но мы про них ещё ничего не утверждали, в том числе что их не может быть два для одного элемента.

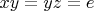
Полезно теперь вернутся к доказательству равенства левого и правого обратного. Правого обратного пока нет, но выражение $x(yz)=(xy)z$, где $xy=yz=e$ можно трактовать не как, что $z$ является правым обратным к $y$ (как это было сделано при доказательстве), а что $x$ - левый обратный к $y$, но $y$ - левый обратный к $z$. Мы успешно ограничились только понятием левого обратного.
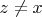
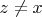
Тогда, рассматривая несимметричные левые обратные, утверждаем что есть такой $y$, что некоторый $x$ - его левый обратный (сущ. по условию), но сам $y$ - левый обратный к $z\neq x$. Может он левый обратный и к $x$, но раз это пара несимметричных левых обратных, как мы это определили, то сущ. $z\neq x$ к которому $y$ левый обратный.

Ну а дальше применяются те же соображения, которые применялись для доказательства того что правый обратный равен левому. Только теперь это не правый обратный, а элемент к которому $y$ является левым обратным. Уже (почти) знаем что этот элемент обязан быть равным левому обратному:

$(*)$
$x(yz)=xe$
$(xy)z=ez=z$

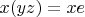
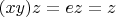
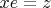
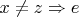
Равенства одновременно верны, если $xe=z$. Тут два варианта: $x=z$, а $e$ - обязано быть нейтральным справа, либо $x\neq z \Rightarrow e$ - не нейтральный справа, ну и тогда левого нейтрального и левого обратного не достаточно для группы, т.е. изначальное утверждение не верно.

Таким образом, задача сводится к доказательству того, что если есть обратный левый и нейтральный левый, то должен быть нейтральный правый.
1. Доказательство для случая - если каждый элемент является левым обратным к себе:
$x(xx)=xe, (xx)x=ex=x \Rightarrow xe=x$, $\forall x\in S$
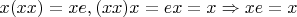
2. Для более общего случая симметричных левых обратных:
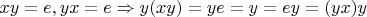
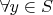
$xy=e,yx=e\Rightarrow y(xy)=ye=y=ey=(yx)y$, $\forall y\in S$, т.к. по условию у любого $y$ есть левый обратный и по дополнительному условию - симметричный.
3. Противоречивость несимметричного левого обратного:
$xy=z\neq e$
$yx = e$
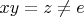
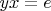
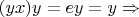
$y(xy)=yz$, $(yx)y=ey=y \Rightarrow$ либо операция не ассоциативна (т.е. противоречие с изначальным условием) либо $yz$ обязано быть $y$ для любого $y$ явл. несимметричным левым обратным. Но тогда и несимметричные левые обратные - симметричные

(Оффтоп)

$z=e\Rightarrow xy=z=e=yx$

Но это не полное доказательство - нужно ещё доказать что $z=e$ - вдруг отличный от $e$ элемент обладает свойствами правого обратного?

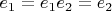
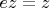
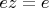
Я помню на том кусочке лекции, которую видел было доказательство, но, правда что не может быть двух нейтральных (предполагается что они оба и левые и правые): $e_1=e_1e_2=e_2$. Но эти же соображения можно применить и только для левых: $ez=z$ - поскольку $e$ - левый нейтр., но в то же время $ez=e$ по вышеуказанному заключению (если $e$ - тоже несимметричный обратный. А если симметричный, то всё равно всё сходится). По другому ещё наверное можно доказать, что $z$ отличный от $a$ такими свойствами обладать не может, потому что типо он точно уже хотя бы в некоторых местах с другими пересекается так что закономерность его как правого нейтрального не соблюдается.

Тогда получается, что если есть симметричные левые обратные, то есть правые нейтральные, а если есть несимметричные, то в итоге их не может быть, то есть они - симметричные, ну а значит - см. первую половину предложения.

А если есть правый нейтральный значит равенства $(*)$ одновременно верны для любых $x,y,z$ таких что $x$ - левый обратный $y$, а $y$ - левый обратный $z$, а по этим равенствам, в таком случае $x=z$, что другими словами означает, что для каждого $y$ существует левый и правый обратный.

-- 14.01.2026, 19:45 --

Резюмируя:
1. Доказываем что есть правый нейтральный
2. Доказываем что правый нейтральный это левый нейтральный
3. Используя 1 и 2 доказываем, что для любых $x,y,z$ таких $x$ - левый обратный $y$, а $y$ - левый обратный $z$, то $z=x$, что означает что у любого $y$ есть левый и правый обратный.

Кстати, сейчас только понял, что из утверждения о том что любой $y$ является левым обратным, и что у него самого есть левый обратный уже следует, что у любого $y$ есть левый и правый обратный (но это не доказывает что они равны).

Тут тогда ещё нужно доказать, почему любой $y$ обязан быть левым обратным кого-то.

[cxzbsdhwert]

Спустя почти два часа я нашёл доказательство того что каждый элемент обязан быть левым обратным кого-то. Ещё раз, по условию - для каждого элемента должен быть левый обратный. Но из этого не следует, что каждый должен быть левым обратным для кого. Все вышеизложенные соображения делались как раз исходя из верности утверждения о том, что каждый элемент является левым обратным.

От обратного: пускай существует элемент не являющийся левым обратным для кого-то. Аккуратное следствие: тогда существует элемент, который является левым обратным для двух разных элементов (ну по крайней мере для конечного множества). Тут можно ошибиться и сделать неверное следствие, что тогда существует элемент у которого два левых обратных - это не обязательно так.

Тогда:
$xa=e$ и $xb=e$.
Докажем что $a=b$:

$$xxba=xxab$$

Пусть $xx=z$

$$zba=zab$$

Тогда $ba$ обязано быть $ab$.
Также $xba=a$, а $xab=b$. Но раз $ab=ba$, то $a=xba=xab=b$, а значит $a=b$.

Тогда резюмирую по новой:
1. Доказываем что любой элемент должен быть левым обратным для кого-то
2. Доказываем что есть правый нейтральный
3. Доказываем что правый нейтральный это левый нейтральный
4. Используя 2 и 3 доказываем, что для любых $x,y,z$ таких $x$ - левый обратный $y$, а $y$ - левый обратный $z$, то $z=x$, что означает что у любого $y$ есть левый и правый обратный

[mihaild]

cxzbsdhwert в сообщении #1714823 писал(а):

Аккуратное следствие: тогда существует элемент, который является левым обратным для двух разных элементов (ну по крайней мере для конечного множества).

Именно что для конечного. А утверждение верно и для бесконечных полугрупп.
Ну и подскажу немного, что Вы правда как-то кругами пошли, есть доказательство без разбора случаев.

[F111mon]

Куча слов вместо конкретного примера.
Вам же подсказали, что можно уложиться в 2 элемента...
Таблиц Кэли 2*2 не так уж много, можно все перебрать и найти вариант, где с одной стороны единица есть, а с другой нет

[cxzbsdhwert]

cxzbsdhwert в сообщении #1714823 писал(а):

$zba=zab$
Тогда $ba$ обязано быть $ab$

Сегодня понял что конечно же это не так. С таким успехом можно было бы изначально утверждать что из того что $xa=e$ и $xb=e$ следует $a=b$.
Тогда всё же остаётся доказать что если в полугруппе есть левый нейтр. и для каждого элемента левый обратный, то каждый элемент сам является левым обратным для кого-то.

F111mon в сообщении #1714858 писал(а):

Таблиц Кэли

Каких "таблиц Кэлли"? Вы первое сообщение в теме видели? Я только кусочек первой лекции посмотрел. Я никаких таблиц Кэлли не знаю. И если Вы первое сообщение читали, значит Вами предложенная для решения задача должна решаться только зная что такое: множество, бинарная операция, полугруппа, моноид и группа.

F111mon в сообщении #1714858 писал(а):

Куча слов вместо конкретного примера. Вам же подсказали...

Да нет, написали наоборот что есть решение основывающееся не на "конкретном примере":

mihaild в сообщении #1714839 писал(а):

есть доказательство без разбора случаев

[mihaild]

cxzbsdhwert в сообщении #1714882 писал(а):

Да нет, написали наоборот что есть решение основывающееся не на "конкретном примере"

Я так понимаю, F111mon говорит о первой задаче - что левого нейтрального недостаточно для моноида. А мой комментарий был ко второй - что левого нейтрального и левого обратного достаточно для группы.

И как раз к задачам первого вида решения разумно искать в виде конкретного контрпримера. А второго - нет, поскольку мы должны описать охватить все полугруппы. Вы конечно можете рассмотреть случаи "а вдруг элемент обратен себе? а вдруг элемент обратен к своему обратному? а вдруг не обратен?", но я подсказываю, что это 1) не обязательно; 2) скорее всего никуда не приведет.

[cxzbsdhwert]

mihaild в сообщении #1714883 писал(а):

Я так понимаю, F111mon говорит о первой задаче - что левого нейтрального недостаточно для моноида.

Так я же её давно решил - предъявил операцию $(x,y)\rightarrow y$. Эту подзадачу предложили Вы, если я правильно понял:

mihaild в сообщении #1714651 писал(а):

cxzbsdhwert в сообщении #1714647 писал(а):

F111mon задачу сформулировал не уточняя аксиом, видимо этого достаточно.

Поскольку задача на "подумать", то доформулировать её - часть упражнения.
Пусть у нас есть полугруппа. Докажите, что:
1. В ней может быть левый нейтральный, но не быть правого нейтрального.
2. Если есть левый нейтральный и есть левый обратный, то это группа.

Поэтому вряд ли F111mon про неё.

-- 15.01.2026, 15:04 --

mihaild в сообщении #1714883 писал(а):

Вы конечно можете рассмотреть случаи

Нет, ну это не то же самое что приводить контрпримеры. Задача, как я понимаю (если использовать только багаж знаний который я обозначил, ещё раз повторю) несколько более комплексная - для доказательства изначального утверждения может понадобится доказать некоторые промежуточные.
Вот как например для доказательства коммутативности операции сложения натуральных чисел в аксиоматике Пеано, то есть что $a+b=b+a$, необходимо сначала доказать целых два промежуточных утверждения, без которых главное не доказать (хотя там это более прямолинейно).