Задача. Пусть

дифференцируема на интервале

, содержащем ноль, и пусть

- последовательность в

такая, что
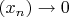
и
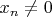
для всех

. Если
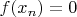
для всех

, показать, что

и

.
С первым равенством легко. А вот с

застрял. Дошел до того, что по теореме Ролля можно выделить последовательность
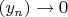
на которой
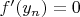
, из чего следует
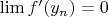
. Но, насколько я понимаю, этого недостаточно чтобы утверждать

, поскольку производная не обязана быть непрерывной.
Была мысль, что может быть теорема Дарбу о промежуточном значении позволит наложить необходимое ограничение, но тут тоже как-то не выходит.
Другой заход, это написать по определению
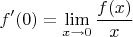
но дальше тоже непонятно, что с этим делать. Мы знаем, что этот предел существует, но как доказать, что он равен нулю?