DedekindЯ тоже вначале хотел это сказать. Но решил сказать так:
Ну, из существования точки

такой, что
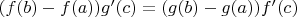
и справедливости
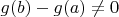
и
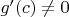
в этой точке, разумеется, следует, что для этой точки

справедливо

.
Просто обычно теорему Коши и формулируют, и доказывают без упоминания равенства
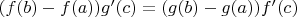
. Это часто удобно, и тогда формулировка теоремы Коши как она есть - вполне естественна.
Да, можем, но тогда удобнее её вообще формулировать не на языке равенства отношений, а на языке
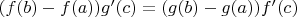
. Это будет короче и яснее.
Формально, если опираться на предварительно доказанную теорему о существовании точки

такой, что
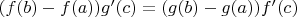
, можно сформулировать теорему Коши на языке отношений как Вы хотели, потребовав
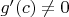
именно в этой точке

(в хотя бы одной из таких точек

, говоря точнее) - только это будет тривиально и не нужно.
-- 11.01.2026, 23:04 --нельзя, потому что теорема не дает способа узнать точку

, а только гарантирует ее существование. Поэтому, нет способа установить, что действительно
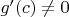
Чисто формально, можно, хотя действительно незачем