В том же примере на картинке в Википедии (с красной секущей и зелёной касательной) вполне может получиться так, что хотя касательная и существует, но в точке касания
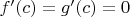
и равенство в теореме Коши не выполнено, так как левая часть в нём не имеет смысла.
Да, я это понимаю, на ноль делить нельзя. Просто
dgwuqtj сказал, что
Можно вообще не требовать

и

, всё и так работает.
Вот я и удивился, как так.
В том же примере на картинке в Википедии (с красной секущей и зелёной касательной) вполне может получиться так, что хотя касательная и существует, но в точке касания
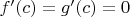
и равенство в теореме Коши не выполнено, так как левая часть в нём не имеет смысла.
Ну вот для данной кривой касательная есть, и деления на ноль нет, все в порядке. И, тем не менее, я же правильно понимаю, что формально она не подпадает под условие теоремы
Теорема: пусть функции

и

непрерывны на
![$[a,b]$ $[a,b]$](https://dxdy-04.korotkov.co.uk/f/f/e/4/fe477a2781d275b4481790690fccd15f82.png)
и дифференцируемы на

и при этом для всех
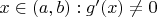
. Тогда существует точка

такая что
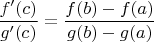
потому что где-то в другой ее точке

?
Поэтому и был вопрос из стартового сообщения, можно ли ослабить условие вот так:
Скажем, потребовать, чтобы
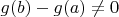
и
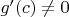
только в той точке

, в которой выполняется
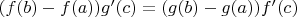
?
чтобы и деления на ноль не возникало, и такие кривые тоже рассматривать?