Новогодняя задача 2026

[nnosipov]

а) Докажите, что уравнение $x^4-2026y^4=1$ имеет только тривиальные решения $x=\pm 1$, $y=0$ в целых числах.

б) А уравнение $x^4-2026y^2=1$ имеет нетривиальные решения в целых числах?

Комментарий. Сюжет старенький (и поэтому может показаться скучным), но классический. Увы, ничего более приличного сочинить не удалось.

Всех с наступающим Новым годом!

[Shadow]

С Новым годом!
По первому пункту, если $x^4>1$, то для $x^2+1$ остаются два варианта: $x^2+1=2026u^4$, но тогда $x^2-1=v^4$ - тривиально.

$x^2+1=2u^4$ - известное уравнение (но не тривиальное), имеет одно нетривиальное решение $(239,13)$, но оно не подходит под Новый год.

nnosipov в сообщении #1713738 писал(а):

б) А уравнение $x^4-2026y^2=1$ имеет нетривиальные решения в целых числах?

Очень надеюсь что нет, а то искать квадраты в решениях Пелля (да еще с таким коэффициентом) дело неблагодарное. Можно попробовать спуском доказать, что не имеет решений $x^4-z^4=2026y^2$.
Если получится, то и подусловие а) автоматически решается. Когда останется свободное время попробую...

[nnosipov]

Shadow
Рад приветствовать в новом году! В пункте а) есть решение без ссылки на уравнение Лююнгренна (не уверен, переборщил или недоборщил я с удвоенными буквами; у этого товарища все трудное, даже фамилия)) А в пункте б) лучше сразу пошире посмотреть, должно проясниться.

[ex-math]

Добрый день!
Пункт а) вроде бы получился у меня методом спуска
Пункт б) как решить не понимаю, но нашел теорему (она непросто доказывается), которая утверждает, что если решение есть, то это либо первое, либо второе решение уравнения Пелля. Соответственно, в этом случае решений нет. Приложу файл с теоремой

Вложение:

aa7847.pdf

[nnosipov]

ex-math
Ваше появление на форуме --- настоящий подарок! Чертовски рад!

ex-math в сообщении #1714054 писал(а):

Пункт а) вроде бы получился у меня методом спуска

Да, так и есть

ex-math в сообщении #1714054 писал(а):

Пункт б) как решить не понимаю, но нашел теорему (она непросто доказывается), которая утверждает, что если решение есть, то это либо первое, либо второе решение уравнения Пелля. Соответственно, в этом случае решений нет.

Такое решение, скорее всего, возможно (не могу скачать файл, причуды теперешней ситуации), я понимаю, о чем идет речь. Я, конечно, напишу, что имелось в виду в пункте б). Но вдруг еще один неравнодушный участник (swec) захочет написать, поэтому пока подождем)

Да, в пункте б) нетривиальных решений тоже нет, все верно.

-- Пн янв 05, 2026 23:39:33 --

Похоже, это статья из Acta Arith., но у поляков сейчас хрен чего скачаешь, даже через dxdy ((

[wrest]

nnosipov в сообщении #1714072 писал(а):

Похоже, это статья из Acta Arith., но у поляков сейчас хрен чего скачаешь, даже через dxdy ((

Попробуйте глянуть тут:

[nnosipov]

wrest
Спасибо, но тоже не получается скачать.

[wrest]

nnosipov в сообщении #1714116 писал(а):

Спасибо, но тоже не получается скачать.

Там три страницы, можно на экране почитать - на экране то видно? Вот прямая ссылка на картинку https://i.ibb.co/6chpLW9K/aa7847.png

[nnosipov]

wrest
Не прогружается картинка(

А, вот название статьи и автор прогрузились, но это пока максимум.

[wrest]

nnosipov
странно это, у меня без впн все норм.
вот ссылка на яндекс диск: https://disk.yandex.ru/i/_1LIXr58KVHbjg

[nnosipov]

wrest
Вот теперь скачал, спасибо. Да, какие-то странные вещи с файлами происходят.

[rightways]

а тут пифагоровый спуск или пелля используется?

[ex-math]

Я использовал уравнение $x^2+2026y^2=z^2$.

[nnosipov]

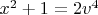
Понятно, что п. а) задачи вытекает из п. б), но сам по себе п. а) может быть решен стандартным рассуждением (метод бесконечного спуска). Пример такого рода см. здесь: Задача 5215 // Математика в школе. 2011. № 8. С. 75. Как правильно заметил Shadow, в процессе спуска возникает классическое уравнение $x^2+1=2v^4$ (Ljunggren’s equation), что позволяет оборвать спуск. Однако, насколько мне известно, Ljunggren’s equation не имеет простого элементарного решения.

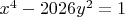
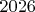
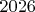
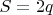
Что касается п. б), то здесь нужно решать уравнение сразу в рациональных числах. Можно показать, что утверждение о том, что уравнение $x^4-2026y^2=1$ имеет в рациональных числах только тривиальные решения, эквивалентно тому, что $2026$ не является конгруэнтным числом. В свою очередь, последнее тоже можно доказывать в более общем виде --- вместо $2026$ взять любое число $S=2q$, где $q \equiv 5 \pmod{8}$ --- простое число. То, что такие числа $S$ не являются конгруэнтными, впервые заметил, по-видимому, A. Genocchi (примерно 1870-е годы). Доказательство элементарное и тоже проводится методом бесконечного спуска.

Способ решения п. б), предложенный ex-math, тоже, разумеется, правильный, но, на мой взгляд, там кухня гораздо более тонкая.