О одном дифференциальном уравнении

[pan555]

У меня ко всем математический вопрос :
Известно следующее дифференциальное уравнение в частных производных :
$ d^2F(x,y,z)/d^2x + d^2F(x,y,z)/d^2y + d^2F(x,y,z)/d^2z = p $
(Это уравнение Пуассона вроде?)
А занимался ли кто нибудь дифференциальным уравнением в частных производных следующего вида :
$d^4F(x,y,z)/d^4x + d^2F(x,y,z)/d^2x + d^4F(x,y,z)/d^4y + d^2F(x,y,z)/d^2y + d^4F(x,y,z)/d^4z + d^2F(x,y,z)/d^2z $ ?

[Ende]

Тема перемещена из форума «Математика (общие вопросы)» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы)

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.

[Ende]

Тема перемещена из форума «Карантин» в форум «Математика (общие вопросы)»
Причина переноса: не указана.

[realeugene]

pan555 в сообщении #1713432 писал(а):

дифференциальное уравнение в частных производных

Частные производные записываются при помощи символа "\partial": $\partial$

[pan555]

realeugene в сообщении #1713461 писал(а):

pan555 в сообщении #1713432 писал(а):

дифференциальное уравнение в частных производных

Частные производные записываются при помощи символа "\partial": $\partial$

Отредактировать уже не могу,увы..

[Mikhail_K]

realeugene в сообщении #1713461 писал(а):

Частные производные записываются при помощи символа "\partial": $\partial$

(Оффтоп)

И кроме того, не $\frac{\partial^2 F}{\partial^2 x}$, а $\frac{\partial^2 F}{\partial x^2}$.

[Ende]

pan555

$$ \dfrac{\partial^4F(x,y,z)}{\partial x^4} +\dfrac{\partial^2F(x,y,z)}{\partial x^2} + \dfrac{\partial^4F(x,y,z)}{\partial y^4} +\dfrac{\partial^2F(x,y,z)}{\partial y^2} + \dfrac{\partial^4F(x,y,z)}{\partial z^4} + \dfrac{\partial^2F(x,y,z)}{\partial z^2} = p $$

Это то, что Вы хотели?

[pan555]

Ende в сообщении #1713481 писал(а):

pan555

$$ \dfrac{\partial^4F(x,y,z)}{\partial x^4} +\dfrac{\partial^2F(x,y,z)}{\partial x^2} + \dfrac{\partial^4F(x,y,z)}{\partial y^4} +\dfrac{\partial^2F(x,y,z)}{\partial y^2} + \dfrac{\partial^4F(x,y,z)}{\partial z^4} + \dfrac{\partial^2F(x,y,z)}{\partial z^2} = p $$

Это то, что Вы хотели?

Да,совершенно верно !!!

[Red_Herring]

Ну что? Эллиптическое уравнение 4го порядка. Если область прямоугольный параллелепипед, то можно разделить переменные. Больше ничего интересного не видно.

[pan555]

Red_Herring в сообщении #1713531 писал(а):

Ну что? Эллиптическое уравнение 4го порядка. Если область прямоугольный параллелепипед, то можно разделить переменные. Больше ничего интересного не видно.

Где можно посмотреть решения этого уравнения типа центрально симметричного ?
( как в уравнении Пуассона - ибо если в рассматриваевом уравнении удалить члены 4 - го порчдка, то и получится уравнение Пуассона)

[worm2]

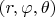
Для центрально-симметричного случая нужно перевести оператор в сферические координаты $(r, \varphi, \theta)$. Затем убрать все члены, содержащих производные по $\varphi$ и по $\theta$, останутся только по $r$. Получится обыкновенный дифур по $r$.
Это весьма муторно.
Вероятно, человек с намётанным глазом сразу сможет выписать полученный дифур (я к таковым не отношусь).
Наверное, это также можно сделать с помощью системы компьютерной алгебры типа Mathematica, но у меня тоже с наскока не получилось разобраться.
Я бы, если бы передо мной встала такая задача, спросил бы совета на англоязычном форуме типа mathematica.stackexchange.com. Тамошний народ весьма искушён и в ручном дифференцировании, и в машинном.
Но — опять закавыка, нужно знать английский язык.
В общем, куда ни кинь, нужны собственные серьёзные усилия.
А, и это не говоря о том, что получившийся обыкновенный дифур тоже нужно суметь решить.

[pan555]

Уважаемый worm2!
Весьма полезные советы.
Выход у меня только один - претворить эти советы в дело.
Придется самому всё делать ,ибо с английским у меня не очень..
Где могут быть описаны самые эффективные алгоритмы перевода оператора в сферичесаие координаты ?
И если удасться перевести в обычный дифур - то ситуация для меня сильно упростится.
Так что прошу советов...

[Dedekind]

pan555 в сообщении #1713541 писал(а):

с английским у меня не очень

Вот бы существовали онлайн-переводчики. Они бы очень облегчили дело.

[пианист]

worm2 в сообщении #1713540 писал(а):

Для центрально-симметричного случая нужно перевести оператор в сферические координаты $(r, \varphi, \theta)$. Затем убрать все члены, содержащих производные по $\varphi$ и по $\theta$, останутся только по $r$.

Все правильно, только если нам нужно центральносимметричное, то от углов оно не должно зависеть. Другими словами, должно быть $F = u(x^2+y^2+z^2)$. Но если это подставить в уравнение, вылезет член вида $u^{(4)} \cdot(x^4+y^4+x^4)$. Так что облом.

Upd подразумевалась сферическая симметрия.

[pan555]

пианист в сообщении #1713545 писал(а):

worm2 в сообщении #1713540 писал(а):

Для центрально-симметричного случая нужно перевести оператор в сферические координаты $(r, \varphi, \theta)$. Затем убрать все члены, содержащих производные по $\varphi$ и по $\theta$, останутся только по $r$.

Все правильно, только если нам нужно центральносимметричное, то от углов оно не должно зависеть. Другими словами, должно быть $F = u(x^2+y^2+z^2)$. Но если это подставить в уравнение, вылезет член вида $u^{(4)} \cdot(x^4+y^4+x^4)$. Так что облом.

Получается,что если и решить задачу для центральносимметрического случая, то нужно переопределить определение расстояния ? (Типа не сумма квадратов,а сумма "четырков" ?)