Задача на определение конкретной кривой

[pan555]

Доброого времени суток !
Имеeтся следующая задача.
Задана параметрически пространственная кривая по следующей формуле :

$$ $$x= c_1_1\cdot \sin(w\cdot s) +c_1_2\cdot \cos(w\cdot s) + c_1_3\cdot s +c_1_4 $$ $$y = c_2_1\cdot \sin(w \cdot s) +c_2_2 \cdot \cos(w \cdot s) + c_2_3 \cdot s +c_2_4 $$ $$z = c_3_1\cdot \sin(w \cdot s) +c_3_2\cdot \cos(w \cdot s) + c_3_3\cdot s +c_3_4 $$ $$

где s-параметр.
Сколько нужно задать точек с координатами (x,y,z), что бы определить конкретные
значения $ c_i_j $ ?
(Если бы таким образом была задана прямая, то нужно 2 точки,так?)

[dgwuqtj]

Здравствуйте. Если взять даже бесконечно много точек $(1, 0, n)$ при всех целых $n$, то они не задают кривую однозначно. Подходят
\begin{align*} x &= \cos 2 \pi s, \\ y &= \sin 2 \pi s, \\ z &= c s \end{align*}
для всех $c = \frac 1 k$, $k \in \mathbb N$.

[pan555]

dgwuqtj в сообщении #1712895 писал(а):

Здравствуйте. Если взять даже бесконечно много точек $(1, 0, n)$ при всех целых $n$, то они не задают кривую однозначно. Подходят
\begin{align*} x &= \cos 2 \pi s, \\ y &= \sin 2 \pi s, \\ z &= c s \end{align*}
для всех $c = \frac 1 k$, $k \in \mathbb N$.

Почему ?
Мне кажется ,для $c_i_j$ это 12 чисел - это 4 точки (4 × 3 координаты) + для каждой точуи своё значенип s -
Итого 6 точек.
В чём я ошибаюсь ?

[dgwuqtj]

pan555 в сообщении #1712896 писал(а):

Почему ?

Потому что если подставить такие $c$, то все точки действительно окажутся на кривой.

pan555 в сообщении #1712896 писал(а):

В чём я ошибаюсь ?

В том, что не любой набор из 36 уравнений на параметры и 12 значений $s$ имеет единственное решение. С линейной алгеброй знакомы?

[pan555]

dgwuqtj в сообщении #1712901 писал(а):

pan555 в сообщении #1712896 писал(а):

Почему ?

Потому что если подставить такие $c$, то все точки действительно окажутся на кривой.

pan555 в сообщении #1712896 писал(а):

В чём я ошибаюсь ?

В том, что не любой набор из 36 уравнений на параметры и 12 значений $s$ имеет единственное решение. С линейной алгеброй знакомы?

С линейной алгеброй знаком.
Я так понимаю, для определения $c_{ij}$ нужны 36 уравнений ,если исходить из фиксации 4 точек.
Но у нас тогда остается необходимость определить 4 значения параметра s.
Тогда добавим ещё одну точку - это ещё 3 уравнения и ещё одно значение параметра s.
Отсюда получается,что для полного определения конкретной кривой по таким формулам достаточно 5 точек.

[dgwuqtj]

Вот система уравнений, из которой вы пытаетесь найти параметры, не является линейной. А если бы она была линейной, пришлось бы проверять невырожденность.

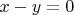
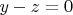
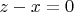
Пример: из трёх уравнений $x - y = 0$, $y - z = 0$, $z - x = 0$ неизвестные найти тоже нельзя. Хотя их 3 и уравнений 3.

-- 20.12.2025, 12:26 --

Если уж заниматься подсчётами уравнений и неизвестных, то я бы скорее ожидал, что через 6 точек общего положения проходит не более чем счётный набор спиралей. Но, опять же, это просто интуитивное соображение.

Для алгебраических кривых ситуация похожая: окружность задаётся 3 точками общего положения (не лежащими на одной прямой), невырожденная коника — 5 точками (никакие 3 точки не на одной прямой), а коника с возможным вырождением в пару прямых (параллельных или пересекающихся, но не совпадающих) — 5 точками, никакие 4 из которых не лежат на одной прямой.

[svv]

pan555
1) Значение $w$ известно?
2) Верно ли я понимаю правила игры? На каждое выбранное нами $s_i$, где $i=1, 2, 3, ...$, нам сообщают тройку $(x(s_i), y(s_i), z(s_i))$. Таким образом, для каждой тройки мы знаем и $s_i$. Какое минимальное число попыток необходимо для гарантированного определения всех коэффициентов?

[pan555]

svv в сообщении #1713318 писал(а):

pan555
1) Значение $w$ известно?
2) Верно ли я понимаю правила игры? На каждое выбранное нами $s_i$, где $i=1, 2, 3, ...$, нам сообщают тройку $(x(s_i), y(s_i), z(s_i))$. Таким образом, для каждой тройки мы знаем и $s_i$. Какое минимальное число попыток необходимо для гарантированного определения всех коэффициентов?

Задача стоит так :
Одна точка определяется тройкой $(x(s_i), y(s_i), z(s_i))$, причем известны только координаты - и всё.
Зпдача состоит в том,что бы выяснить,сколько нужно точек,что бы определить все параметры уравнения этой конкретной кривой.
И я думаю,что я эту задачу решил - но решение займет место ,как статья.
И не знаю, можно ли тут выложить этот большой текст ?
И будет ли тут это кому интересно,кроме меня ?

[EXE]

pan555 в сообщении #1712894 писал(а):

Если бы таким образом была задана прямая, то нужно 2 точки,так?

А сколько будет уравнений, если бы речь шла о параметрическом задании прямой в пространстве?

[pan555]

EXE в сообщении #1713488 писал(а):

pan555 в сообщении #1712894 писал(а):

Если бы таким образом была задана прямая, то нужно 2 точки,так?

А сколько будет уравнений, если бы речь шла о параметрическом задании прямой в пространстве?

Для параметрического задания прямой в 3-х мерном пространстве нужно 3 уравнения - это 6 констант , общих для всех точек конкретной прямой и 1 параметр, определяющий конкретную точку конкретной прямой.
Если задаем 2 точки в 3-х мерном пространстве - то это 6 координат - и тем самым они точно определчют конкретную прямую а 3-х мерном пространстве.
Учтите,что сам параметр можно определить через координаты и константы,общие для всех точек конкретной прямой.

[EXE]

pan555 в сообщении #1713489 писал(а):

Для параметрического задания прямой в 3-х мерном пространстве нужно 3 уравнения - это 6 констант , общих для всех точек конкретной прямой и 1 параметр.

Не-не, я же о системе, с помощью которой будут определены константы. Ну, по аналогии с Вашей задачей о кривой.

[pan555]

EXE в сообщении #1713490 писал(а):

pan555 в сообщении #1713489 писал(а):

Для параметрического задания прямой в 3-х мерном пространстве нужно 3 уравнения - это 6 констант , общих для всех точек конкретной прямой и 1 параметр.

Не-не, я же о системе, с помощью которой будут определены константы. Ну, по аналогии с Вашей задачей о кривой.

Если аналогия, то система такая :
$ $$x= c_1_1* s +c_1_2$$ $$y = c_2_1* s +c_2_2$$ $$z = c_3_1* s +c_3_3 $$ $
Всё примитивно решается.

[EXE]

pan555 в сообщении #1713491 писал(а):

Если аналогия, то система такая :

Формально уравнений должно быть 6. При этом параметр является 7-й переменной. То есть, система из 6 уравнений относительно 7 переменных, которая просто решается, потому что мы знаем начальную точку при значении параметра=0. Если перейти к параметрической сфере, то 4 точки нам дают 12 уравнений при 6 переменных. Из системы надо исключить параметры и должно остаться 4 искомых переменных. То есть, мне кажется, при составлении системы надо учитывать параметры в качестве переменных.

[pan555]

Рассмотрим исходную систему :

$$ $$x= c_1_1\cdot \sin(w\cdot s) +c_1_2\cdot \cos(w\cdot s) + c_1_3\cdot s +c_1_4 $$ $$y = c_2_1\cdot \sin(w \cdot s) +c_2_2 \cdot \cos(w \cdot s) + c_2_3 \cdot s +c_2_4 $$ $$z = c_3_1\cdot \sin(w \cdot s) +c_3_2\cdot \cos(w \cdot s) + c_3_3\cdot s +c_3_4 $$ $$

Величины $ c_1_1. ...c_3_4 $ определяют всю кривую, назовем их общими.
Величины $ \sin(w\cdot s) , \cos(w\cdot s) ,s. $ опредеделяют конкретную точкв на этой кривой, назовём их локальными.
Задав одну точку (3 координаты),можно выразить локальные величины через координаты и общие величины.
А далее, задав еще 3 точки - итого 4 точки (12 уравнений), можем уже определить и общие величины через координаты 4 точек.
В итоге задача решена. Для точного определения конкретной кривой заданного типа достаточно 4 точек .
А то,что эти точки не должны лежать в одной плоскости и любые 3 из них не должны лежать на одной прямой ,это требует своего доказательства.

[realeugene]

pan555 в сообщении #1712894 писал(а):

Сколько нужно задать точек с координатами (x,y,z), что бы определить конкретные
значения $ c_i_j $ ?

Сколько неизвестных и какие? Для каждой заданной точки не известен свой параметр $s$ и 12 общих для всех точек линейных коэффициентов? При этом известна общая $w$ и по три координаты на каждую точку?