Ну и сложу (кавычки по вкусу), и получу
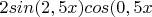
). Вполне возможно, что при решении конкретной задачи именно так было бы максимально удобно её решать. А с "этими Вашими порядками" у ТС вообще вполне себе может сложиться впечатление, что ничего такого до вычисления каждого из синусов делать нельзя.
Ну вот сложили Вы синусы, получили произведение, ну не будете же Вы теперь наступать на горло собственной песне, и находить сначала синус и косинус, а потом перемножать их, как того требует естественный порядок действий?
Вы же сначала предлагаете, насколько я понял, умножить синус на косинус, и получить обратно сумму тех же исходных синусов, и дальше гонять по кругу сумму в произведение, и произведение обратно в сумму, пока не надоест, а уже потом сначала подставить аргументы в исходное выражение, и уже полученные промежуточные результаты, либо сложите, либо перемножить, в зависимости от того, на каком шаге наступило просветление...
Сложил, как Вы мне сами и предлагали, и получил (хотя по-Вашему это невозможно, или как?) тождественно равное выражение. И единственный при этом известный мне "естественный порядок действий" - тот, о котором читал последний раз в учебнике максимум за 7 класс. Т.е. примерно
такой.
Ну и что получается то. Хотим - находим сначала значения всех функций в выражении. Хотим - сначала преобразовываем в какое угодно тождественное выражение, а потом находим значения всех функций. Хотим - находим вперемешку с тождественными преобразованиями. Ну так и где этот Ваш особый "естественный порядок" для выражений с функциями, по которому их надо находить строго на определённом этапе? : )
(Оффтоп)
Вот серьёзно...ТС пишет, что ей не понятно к чему применять "действие sin" в выражении

, и "выносит за скобки"

, получая

. А ей вместо того, чтобы отправить разбираться в самой начальной теории по функциям (и вообще последовательно осваивать алгебру с 7-го класса) на серьёзных щах объясняют, что так нельзя из-за "порядка действий".
