Почему это доказательство полноты R не подходит для Q?

[cxzbsdhwert]

Аксиома полноты: если у некоторого множества есть 2 подмножества $A$ и $B$ такие что для $\forall b \in B$, $a \leq b | a \in A$, то на множестве выполняется аксиома полноты если $\exists c: \forall a\in A \forall b\in B, a \leq c \leq b$.

Утверждается, что на множестве всех бесконечных десятичных дробей вида $a_0.a_1a_2...$, которое является моделью множества вещественных чисел, аксиома полноты выполняется.

Доказывается так: строим $c$: $c_0$ - наименьшее $b_0$ среди всех элементов "большего" множества $B$. $c_1$ - наименьшее $b_1$ среди всех $b$ с $c_0$ в качестве $b_0$. И так далее. Полученное $c$ больше либо равно любого $a$ и меньше либо равно любого $b$.

Вопрос: почему то же самое нельзя сделать с множеством рациональных чисел, представив их как бесконечные десятичные дроби (нули добавлять для конечных дробей), даже для того же тривиального примера с корнем из двух?

Я правильно понимаю, что вышеизложенное доказательство буквально предлагает выбрать наименьший элемент. А так можно? Для интервала, в частности.

[dgwuqtj]

cxzbsdhwert в сообщении #1712941 писал(а):

если у некоторого множества есть 2 подмножества

Забыли добавить, что $A, B \neq \varnothing$.

cxzbsdhwert в сообщении #1712941 писал(а):

Вопрос: почему то же самое нельзя сделать с множеством рациональных чисел, представив их как бесконечные десятичные дроби (нули добавлять для конечных дробей), даже для того же тривиального примера с корнем из двух?

Потому что полученное $c$ не обязано быть рациональным. То есть если мы говорим про десятичные дроби, никто не гарантирует его периодичность.

cxzbsdhwert в сообщении #1712941 писал(а):

Я правильно понимаю, что вышеизложенное доказательство буквально предлагает выбрать наименьший элемент. А так можно? Для интервала, в частности.

Для интервала $(0, 1)$ будет выбрано число $0$. То есть не наименьший элемент, а инфимум.

[cxzbsdhwert]

dgwuqtj в сообщении #1712943 писал(а):

Потому что полученное $c$ не обязано быть рациональным. То есть если мы говорим про десятичные дроби, никто не гарантирует его периодичность.

1. А как доказать, что выбранное по такому принципу $c$ рационально, для случая $A=(0,1);B=(1,2)$, $c$ ведь в таком случае $1$ (но из доказательства выше это по-моему не следует), и иррационально для случая $A=(0,\sqrt{2});B=(\sqrt{2},3)$?

2. И почему инфинум $B$ а не именно наименьший $B$? По схеме, последовательность всех разрядов десятичной дроби $c$ совпадает с последовательностью всех разрядов некоторого $b\in B$, следовательно $c\in B$.

3. И ещё: я понимаю, что, например для $B=(1,2)$ перебирая наименьшие $b\in B$, это будет происходить бесконечно, и $c$ бесконечно будет пополняться новыми нулевыми разрядами. То есть невозможность найти наименьшее $b$ обосновывается бесконечностью процесса составления $c$. Но почему мы тогда по такому бесконечному процессу получаем конечное $c$, удовлетворяющее аксиоме полноты (для $\mathb R$)?

[dgwuqtj]

cxzbsdhwert в сообщении #1712944 писал(а):

1. А как доказать, что выбранное по такому принципу $c$ рационально, для случая $A=(0,1);B=(1,2)$, $c$ ведь в таком случае $1$ (но из доказательства выше это по-моему не следует), и иррационально для случая $A=(0,\sqrt{2});B=(\sqrt{2},3)$?

Вы спрашиваете, как доказать, что $1$ рационально, а $\sqrt 2$ иррационально? Первое по определению, у второго утверждения доказательство стандартное. В общем виде, если у вас просто какие-то два множества как-то заданы, вы не сможете понять, рациональна или иррациональна точка $c$ (технически эта задача алгоритмически неразрешима, если ограничиться случаем перечислимых $A, B \subseteq \mathbb Q$).

cxzbsdhwert в сообщении #1712944 писал(а):

2. И почему инфинум $B$ а не именно наименьший $B$? По схеме, последовательность всех разрядов десятичной дроби $c$ совпадает с последовательностью всех разрядов некоторого $b\in B$, следовательно $c\in B$.

Потому что вы сами привели пример, в случае $B = (1, 2)$ наименьшего элемента нет.

cxzbsdhwert в сообщении #1712944 писал(а):

3. И ещё: я понимаю, что, например для $B=(1,2)$ перебирая наименьшие $b\in B$

Вы перебираете элементы пустого множества.

-- 20.12.2025, 18:08 --

cxzbsdhwert в сообщении #1712944 писал(а):

$c$ бесконечно будет пополняться новыми нулевыми разрядами. То есть невозможность найти наименьшее $b$ обосновывается бесконечностью процесса составления $c$.

Это ещё почему? Число $c$ не меняется, тут нет никакого течения времени. К тому же в случае $B = [1, 2]$ число $c$ получается абсолютно точно так же.

[cxzbsdhwert]

dgwuqtj в сообщении #1712947 писал(а):

Вы спрашиваете, как доказать, что $1$ рационально, а $\sqrt 2$ иррационально?

Нет, я просто уточнил что нам заведомо известно что такой элемент - единица, и единица, безусловно представима в виде отношения двух натуральных чисел.
Я спросил, как доказать, не зная заведомо что это единица, что получаемый для такого случая $c$ будет рациональным. Видимо для общего случая $A=(a_1,a_2),B=(b_1,b_2),A\leq B$, среди множества $c$ таких что удовлетворяют $a\in A \leq c \leq b \in B$ не будет рациональных тогда, когда $a_2$ и $b_1$ оба одновременно иррациональны. Ну а доказательство рациональности или иррациональности границ конкретных интервалов, как я понимаю, на аксиому полноты не опирается.

dgwuqtj в сообщении #1712947 писал(а):

Вы перебираете элементы пустого множества.

Может я не ясно выразился, но я имел в виду упорядоченное подмножество $B'$ десятичных дробей $B$, таких что $B'=\{ x^0\in B:x \ni x_0=\min(y_0\in y \in B), x^1\in B: x \ni x_0=x^{0}_{0},x_1=\min(y_1\in y \in B), ... \}$

Ну то есть, так по схеме доказывания.
Так что это множество отнюдь не пусто, является собственным подмножеством множества $B$, и, что самое важное, $c$ по схеме доказывания принадлежит ему, а значит принадлежит и $B$.

[dgwuqtj]

cxzbsdhwert в сообщении #1712966 писал(а):

Видимо для общего случая $A=(a_1,a_2),B=(b_1,b_2),A\leq B$, среди множества $c$ таких что удовлетворяют $a\in A \leq c \leq b \in B$ не будет рациональных тогда, когда $a_2$ и $b_1$ оба одновременно иррациональны.

Контрпример: для $A = (- \sqrt 2, \sqrt 2)$, $B = (3 - \sqrt 2, 3 + \sqrt 2)$ найдётся рациональное $c = 1{,}5$.

cxzbsdhwert в сообщении #1712966 писал(а):

Так что это множество отнюдь не пусто, является собственным подмножеством множества $B$, и, что самое важное, $c$ по схеме доказывания принадлежит ему, а значит принадлежит и $B$.

У вас формула, конечно, ужасная. Но если под $B'$ вы имели в виду множество конечных десятичных дробей, которые продолжают друг друга, то $c$ в этом множестве не лежит, а является результатом склейки всех такикх конечных десятичных дробей. Также $B'$ не подмножество $B$ и, тем более, $c$ не принадлежит $B$ в общем случае.

[wrest]

cxzbsdhwert в сообщении #1712941 писал(а):

если у некоторого множества есть 2 подмножества $A$ и $B$ такие

Не "если есть такие, что", а "для любых таких, что"
Между подмножествами рациональных $(0,1)$ и $(1,2)$ вставляется рациональное (единица) - ок, засчитано. А между подмножествами рациональных $(1,\sqrt{2})$ и $(\sqrt{2},2)$ - рациональное не вставляется -> game over.

[cxzbsdhwert]

dgwuqtj в сообщении #1712970 писал(а):

Контрпример: для $A = (- \sqrt 2, \sqrt 2)$, $B = (3 - \sqrt 2, 3 + \sqrt 2)$ найдётся рациональное $c = 1{,}5$.

Да, хорошо, стоит уточнить что утверждение верно для $a_2=b_1$, во всех остальных случаях $A\leq B$, множество из $c$ будет содержать рациональное.

dgwuqtj в сообщении #1712970 писал(а):

У вас формула, конечно, ужасная. Но если под $B'$ вы имели в виду множество конечных десятичных дробей, которые продолжают друг друга, то $c$ в этом множестве не лежит, а является результатом склейки всех такикх конечных десятичных дробей. Также $B'$ не подмножество $B$ и, тем более, $c$ не принадлежит $B$ в общем случае.

Формулой я попытался переписать, множество перебираемых десятичных дробей из $B$.

Берётся дробь с наименьшим по значению первым разрядом - она есть потому что разряд это натуральное число в подмножестве $\mathbb N$ от 0 до 9, а значит по аксиоме Архимеда в таком подмножестве есть наименьшее. Наименьший по номеру разряд, то есть первый, тоже есть по всё той же аксиоме Архимеда, и по самой модели вещественного числа как последовательности (десятичной дроби). Выбирается эта десятичная дробь из $B$ и "записывается" в $B'$. Потом выбирается дробь у которой значение следующего разряда, то есть второго, также наименьшая. Записывается в $B'$. И так далее.

Таким образом $B'$ является подмножеством $B$ - все её дроби взяты ниоткуда, кроме как из $B$. Ну а $i$-тый разряд $c$ по схеме является $i$-тым разрядом $i$-ой дроби из $B'$, от чего и заключаю, что $c\in B' \in B$.

Уточню, что из принципа по которому выбирались дроби, следует, что у $i$-той дроби в $B'$ совпадают все разряды от нуля до $i$ со всеми соответствующими разрядами всех дробей от первой до $i-1$.

[dgwuqtj]

cxzbsdhwert в сообщении #1712972 писал(а):

Таким образом $B'$ является подмножеством $B$ - все её дроби взяты ниоткуда, кроме как из $B$.

Тогда да, конечно.

cxzbsdhwert в сообщении #1712972 писал(а):

Ну а $i$-тый разряд $c$ по схеме является $i$-тым разрядом $i$-ой дроби из $B'$, от чего и заключаю, что $c\in B' \in B$.

Неверно заключаете.

[cxzbsdhwert]

dgwuqtj в сообщении #1712974 писал(а):

Неверно заключаете.

Хорошо, а как насчёт такого:

Вы согласны с утверждением? :

Цитата:

Из принципа по которому выбирались дроби, следует, что у $i$-той дроби в $B'$ совпадают все разряды от нуля до $i$ со всеми соответствующими разрядами всех дробей от первой до $i-1$.

Если да, то $c$ также удовлетворяет этому свойству (все её разряды меньше либо равны соответствующих разрядов всех дробей $B'$).

Если Вы утверждаете, что $c$ тем не менее не принадлежит $B'$, значит есть $i$-тый номер такой что дробь из $B'$ с таким номером имеет подпоследовательность из $m\leq i$ совпадающих с $c$ разрядов, но значение некоторого $k>i$ разряда меньше соответствующего разряда $c$.

Предъявите пожалуйста такой номер $i$.

Если его не предъявить, то мы:
1) Не полагаем верным утверждение о том, что в $B'$ есть дробь меньше чем $c$, и
2) полагаем верным, что $c$ меньше любой дроби из $B'$ (а иначе, опять-таки, предъявите меньшую) и
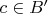
3) теперь, что показать что $c \in B'$, хочется сказать что в $B'$ есть дробь все разряды которой совпадают с $c$, исходя из принципа построения $c$, но нужно предъявить её, а точнее её номер (её мы уже предъявили - это $c$). Либо сказать, что в $B'$ нет дроби, хотя бы один разряд которой отличается от $c$, но это не так.

Короче "ни туда ни сюда"

[dgwuqtj]

cxzbsdhwert в сообщении #1712975 писал(а):

Предъявите пожалуйста такой номер $i$.

Для каких конкретно множеств $B$ и $B'$?

[cxzbsdhwert]

dgwuqtj в сообщении #1712977 писал(а):

cxzbsdhwert в сообщении #1712975 писал(а):

Предъявите пожалуйста такой номер $i$.

Для каких конкретно множеств $B$ и $B'$?

$B'$, в которое отбираются кандидаты на $c$. Ну наверное всё равно тупик, не буду Вас обременять

[dgwuqtj]

cxzbsdhwert в сообщении #1712978 писал(а):

$B'$, в которое отбираются кандидаты на $c$.

Так вы мне его не показываете. В зависимости от $B'$ предъявленный номер $i$ будет разным, а если вы $B'$ описываете у себя достаточно неявно, то и $i$ может быть непредъявимым в принципе.

[cxzbsdhwert]

dgwuqtj в сообщении #1712979 писал(а):

cxzbsdhwert в сообщении #1712978 писал(а):

$B'$, в которое отбираются кандидаты на $c$.

Так вы мне его не показываете. В зависимости от $B'$ предъявленный номер $i$ будет разным, а если вы $B'$ описываете у себя достаточно неявно, то и $i$ может быть непредъявимым в принципе.

$B'$ всегда одинаково для одного и того же $B$, и представляет собой такое упорядоченное множество:

Цитата:

Из $B$ берётся дробь с наименьшим по значению первым разрядом - она есть потому что разряд это натуральное число в подмножестве $\mathbb N$ от 0 до 9, а значит по аксиоме Архимеда в таком подмножестве есть наименьшее. Наименьший по номеру разряд, то есть первый, тоже есть по всё той же аксиоме Архимеда, и по самой модели вещественного числа как последовательности (десятичной дроби). Выбирается эта десятичная дробь из $B$ и "записывается" в $B'$. Потом выбирается дробь у которой значение следующего разряда, то есть второго, также наименьшая. Записывается в $B'$. И так далее.

[dgwuqtj]

По этому описанию $B'$ находится неоднозначно. Например, для $B = (0, 1)$ можно взять $B' = \{ 0{,}1; 0{,}01; 0{,}001; \ldots \}$, а можно $B' = \{ 0{,}2; 0{,}02; 0{,}002; \ldots \}$. А ещё можно взять $B' = \{ 10^{-f(k)} \mid k \in \mathbb N \}$, где $f$ какая-то возрастающая невычислимая функция.