Здравствуйте.
Пусть
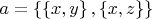
. Тогда ясно, что
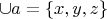
. Пусть теперь
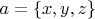
, и нет никакой информации об элементах множеств

(мы не знаем, какие множества принадлежат этим трём множествам). Тогда чему равно

? Вроде бы, простой вопрос, но можно ли на него дать ответ? Спасибо.
P.S. Речь идёт о теории множеств Цермело-Френкеля.
В теории множеств ZF или ZFC все объекты являются множествами, в том числе и ваши

. Поэтому
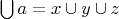
, как Вам и написали. Если, как Вы пишете, про множества

ничего неизвестно, то кроме
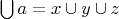
ничего написать нельзя.
Но бывают и теории множеств с атомами. Атомы не являются множествами, хотя могут быть элементами множеств. Во всех теоретико-множественных операциях атомы нужно рассматривать как пустые множества. В частности, если ваши

— атомы, то
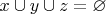
.
То есть, множество, скажем, иррациональных чисел можно представить как объединение всех его элементов?
Результат этого объединения зависит от того, как Вы рассматриваете иррациональные числа. Если Вы имеете в виду модель, построенную в чистой теории множеств, то получится какое-то множество, зависящее от конкретной модели. Если же у Вас числа рассматриваются как атомы, то объединение будет пустым множеством. В обоих случаях результат не выглядит полезным.