Пентадекатлон мечты

[VAL]

Что-то в поиске D(48,23) в последнее время не только журавли в дронтов переродились, но ласточки стали реже попадать в сеть.
Зато последняя - не просто ласточка, но и корректная 21-ка:
18247169589971452699805445117350891564575748224175969041

[Yadryara]

VAL в сообщении #1712039 писал(а):

Зато последняя - не просто ласточка, но и корректная 21-ка:

Здорово! Ух, длиннющая какая, 56 знаков. Стал было её в таблицу помещать — ни в какую. 52-53-значные пока влезали нормально. Пришлось монтировкой.

VAL в сообщении #1712039 писал(а):

ласточки стали реже попадать в сеть.

Ну причина та же самая — ласточкам тоже кислород нужен.

А почему так высоко забрались-то? Опять Ваши полноприводные фокусы?

-- 09.12.2025, 11:46 --

Пожалуй, в 16-ричную систему буду конвертить табличку.

[VAL]

Yadryara в сообщении #1712044 писал(а):

А почему так высоко забрались-то? Опять Ваши полноприводные фокусы?

Никаких фокусов!
Я прикинул статистику. Среди дырявых цепочек длиной 23, дырки, обусловленные нехваткой делителей (24 или даже 12 вместо 48), встречаются примерно в два раза чаще, чем дырки, вызванные избытком делителей. Значит, при поиске надо не скакать по низам, а забираться повыше.

[EUgeneUS]

VAL в сообщении #1712055 писал(а):

Среди дырявых цепочек длиной 23, дырки, обусловленные нехваткой делителей (24 или даже 12 вместо 48), встречаются примерно в два раза чаще, чем дырки, вызванные избытком делителей. Значит, при поиске надо не скакать по низам, а забираться повыше.

Скорее всего, неверный вывод.
Возможно при верном наблюдении.

-- 09.12.2025, 15:43 --

Все асимптотики: $P_{p}(N), P_{pq}(N), P_{pqr}(N), P_{pqrs}(N)$ являются убывающими, при $N>10^{10}$, некоторые - из них ещё раньше.

А наблюдаемый эффект:

VAL в сообщении #1712055 писал(а):

Среди дырявых цепочек длиной 23, дырки, обусловленные нехваткой делителей (24 или даже 12 вместо 48), встречаются примерно в два раза чаще, чем дырки, вызванные избытком делителей.

Это эффект выживших.
Избыток делителей "умирает" на быстрых проверках чаще, чем недостаток делителей. Поэтому в логи избыток делителей попадает реже.

[VAL]

EUgeneUS в сообщении #1712057 писал(а):

Это эффект выживших.
Избыток делителей "умирает" на быстрых проверках чаще, чем недостаток делителей. Поэтому в логи избыток делителей попадает реже.

Возможно, Вы и правы. Но есть и контраргумент. Процент "выживших" с ростом перебираемых чисел не убывает. По крайней мере, с ростом в тех пределах, в которых я веду поиск.

[EUgeneUS]

VAL в сообщении #1712096 писал(а):

Но есть и контраргумент.

Контраргумент к чему?
То, что вероятность найти цепочку за одну проверку падает с ростом чисел в цепочке - это общее место. Давно известное. Подтверждается:
1. И простыми наблюдениями.
2. И общими соображениями про асимптотики ожидаемых чисел в каждой позиции.
3. И численными расчетами.

[Yadryara]

У Демиса нашлись два новых дронтозавра. И один из них принёс ещё две единички в правом крыле:

8276466129185709384898037667333514567718482446345938 11111111111111111 1111   11    23

Всё-таки буду в 64-ричной постить. К обычному цифробуквенному набору добавлю ещё собачку и параграф:

0 — 0
1 — 1
...
9 — 9
10 — a
11 — b
...
35 — z
36 — A
37 — B
...
61 — Z
62 — @
63 — &

[EUgeneUS]

Yadryara в сообщении #1712110 писал(а):

Всё-таки буду в 64-ричной постить.

Ещё можно 360-ричной клинописью, как у древних шумеров.

[VAL]

EUgeneUS в сообщении #1712107 писал(а):

VAL в сообщении #1712096 писал(а):

Но есть и контраргумент.

Контраргумент к чему?
То, что вероятность найти цепочку за одну проверку падает с ростом чисел в цепочке - это общее место. Давно известное. Подтверждается:
1. И простыми наблюдениями.
2. И общими соображениями про асимптотики ожидаемых чисел в каждой позиции.
3. И численными расчетами.

То, что для Вас общее место, для меня ошибочное утверждение.
И это подтверждается:
1. И простыми наблюдениями.
2. И общими соображениями про асимптотики ожидаемых чисел в каждой позиции.
3. И численными расчетами.
Например:

c := 0; for i to 10^6 do n := 10^12+i; if tau(n) = 128 and tau(n+1) = 128 then c := c+1 end if end do; c;
                               13
c := 0; for i to 10^6 do n := 10^20+i; if tau(n) = 128 and tau(n+1) = 128 then c := c+1 end if end do; c;
                              441

То есть, вероятность найти цепочку из 2-х чисел, имеющих по 128 делителей с ростом чисел растет. Причем довольно долго и весьма значительно.
Я не вижу причин, почему для цепочки D(48,23) должна быть принципиально иная картина.
Конечно, когда-нибудь плотность чисел с искомым количеством делителей начнет уменьшаться с ростом чисел. Вопрос - когда?

[Yadryara]

VAL
Не, ну где бузина, а где дядька. Между 128 и 48 огромная разница.

А Вы понимаете что вот здесь считалось? Это ведь конкретный счёт был:

Yadryara в сообщении #1710869 писал(а):

Мне пока что так далеко не нужно, возможно пригодится VALу или Хьюго. Но всё-таки поиск по 1-1-17-4-11!, насколько помню, означает что свободные простые для этой серии паттернов начинаются с 71.

А Вы, как понял, продолжили счёт для свободных, начиная с 67. И для этих простых я таблицы объединил:

10^   For 1e6         2     4     8    16

  40   131600        83   250   312   218
  41   131593        80   244   315   219
  42   131577        77   244   312   224
  43   131565        77   236   309   227
  44   131564        74   234   307   228
  45   131590        73   232   305   230
  46   131585        72   229   302   231
  47   131595        72   223   301   233
  48   131571        68   221   300   236
  49   131576        68   220   298   235
  50   131574        67   217   296   236
  51   131585        65   213   295   240
  52   131581        64   210   295   238
  53   131608        61   207   294   241
  54   131575        62   204   292   241
  55   131598        59   201   290   244
  56   131585        59   198   291   242
  57   131578        58   196   288   245
  58   131606        57   195   284   244
  59   131590        55   191   285   247

[EUgeneUS]

VAL в сообщении #1712150 писал(а):

То есть, вероятность найти цепочку из 2-х чисел, имеющих по 128 делителей с ростом чисел растет. Причем довольно долго и весьма значительно.
Я не вижу причин, почему для цепочки D(48,23) должна быть принципиально иная картина.
Конечно, когда-нибудь плотность чисел с искомым количеством делителей начнет уменьшаться с ростом чисел. Вопрос - когда?

На этот вопрос есть известный ответ:

EUgeneUS в сообщении #1712057 писал(а):

Все асимптотики: $P_{p}(N), P_{pq}(N), P_{pqr}(N), P_{pqrs}(N)$ являются убывающими, при $N>10^{10}$, некоторые - из них ещё раньше.

-- 10.12.2025, 18:18 --

VAL в сообщении #1712150 писал(а):

То есть, вероятность найти цепочку из 2-х чисел, имеющих по 128 делителей с ростом чисел растет. Причем довольно долго и весьма значительно.

Мы не ищем цепочку из 2-х чисел с 128 делителями.
Мы (Вы) даже не ищем цепочку из 23 чисел с 48 делителями, как бы странно это не звучало.
Вы ищете цепочку из 23 чисел, у которых после деления на известные числа, заданные паттерном, в каждом месте будет число имеющее 1, 2, 3 либо 4 делителя (опять же в зависимости от используемого паттерна).

[Yadryara]

EUgeneUS в сообщении #1712167 писал(а):

в каждом месте будет число имеющее 1, 2, 3 либо 4 делителя

Опять голову морочите? 2, 4, 8 или 16 делителей.

[VAL]

Yadryara в сообщении #1712161 писал(а):

VAL
Не, ну где бузина, а где дядька. Между 128 и 48 огромная разница.

Ну не такая уж и огромная. Всего-то 80

EUgeneUS в сообщении #1712107 писал(а):

То, что вероятность найти цепочку за одну проверку падает с ростом чисел в цепочке - это общее место. Давно известное. Подтверждается:

Не вижу в этой цитате упоминания D(48,23).

Впрочем, я конечно же понимал, что речь идет не о любых цепочках.
Просто мои методы полемики косплеят методы оппонента: жестко, резко и... подменяя суть вопроса.
Вот мои аргументы до обострения дискуссии:

VAL в сообщении #1712096 писал(а):

Возможно, Вы и правы. Но есть и контраргумент. Процент "выживших" с ростом перебираемых чисел не убывает. По крайней мере, с ростом в тех пределах, в которых я веду поиск.

Вместо попытки разобраться с указанным феноменом я получил отлуп, как двоечник, не выучивший таблицу умножения.

Между тем, вопрос действительно интересный, и ответ на него мне непонятен. Я даже перепроверил себя: вдруг я что-то напутал с этим самым процентом выживших. И собрал статистику не по 2-м, как раньше, а по 8 комплектам, для которых счет поднялся достаточно высоко.
И да, действительно, результаты оказались немного иные. В тех двух комплектах, на статистику которых я опирался изначально, процент выживших с ростом чисел практически не изменился. А в остальных шести он заметно... возрос. Где-то 1.2 раза, а где-то и 1.5.

Объяснения не знаю. Но вывод, что считать надо, не жестко прижимаясь к низам, напрашивается.

-- 11 дек 2025, 00:32 --

EUgeneUS в сообщении #1712167 писал(а):

На этот вопрос есть известный ответ:
EUgeneUS в сообщении #1712057

писал(а):
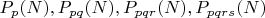
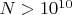
Все асимптотики: $P_{p}(N), P_{pq}(N), P_{pqr}(N), P_{pqrs}(N)$ являются убывающими, при $N>10^{10}$, некоторые - из них ещё раньше.

Спасибо, что напомнили. Я так понимаю, что это данные с учетом взаимной простоты интересующих нас чисел с простыми до 67?
Я припоминаю, что мы это уже обсуждали, но поленился искать.

Но как эти данные согласуются с упомянутой мной статистикой, мне, по-прежнему, непонятно.
Наверняка есть какое-то объяснение. Возможно, очень простое. Но пока я его не вижу.

[Yadryara]

Пока про другое, ибо давно собирался.

Говорил же: не запутаемся. Не то что бы наш счёт подходил к концу, но вот как выглядит текущее состояние счёта в наиболее распутанных 3 группах из всех 162 комплектов при сквозной нумерации:

      32  121  361     от 0 до   % от 10!
                         e50 *           
=========================================   37z
45.    8   18    5         100        100
...    8   18    x         100        100
51.    8   18   19         100        100
52.    8   22    5         100        100
...    8   22    x         100        100
59.    8   22   19         100        100
60.    8   2     5         100        100
...    8   2     x         100        100
67.    8   2    19         100        100
...    8   5     x         100        100
72.    8   5    16         100        100
...    8   5     x          10        100
74.    8   5    19          10        100
75.    8   7     5         100        100
...    8   7     x         100        100
81.    8   7    19         100        100
=========================================   37
82.   15   16    4         100        100
...   15   16    x         100        100
88.   15   16   18         100        100
89.   15   18    4         100        100
...   15   18    x         100        100
95.   15   18   16         100        100
96.   15   21    4         100        100
...   15   21    x         100        100
103.  15   21   18         100        100
104.  15    1    4          50        100
...   15    1    x          50        100
111.  15    1   18          50        100
112.  15    5    4          10        100
...   15    5    x          10        100
118.  15    5   18          10        100
=========================================   44
119.  16   18    5         100        100
...   16   18    x         100        100
125.  16   18   19         100        100
126.  16   22    5          10        100
...   16   22    x          10        100
130.  16   22   13         920        100
...   16   22    x          10        100
133.  16   22   19          10        100
134.  16    2    5          10        100
...   16    2    x          10        100
141.  16    2   19          10        100
142.  16    7    5          10        100
...   16    7    x          10        100
146.  16    7   13         920        100
...   16    7    x          10        100
148.  16    7   19          10        100
149.  16    8    5          10        100
...   16    8    x          10        100
155.  16    8   19          10        100
156.  16   19    5          10        100
...   16   19    x          10        100
161.  16   19   13         100        100
162.  16   19   17          10        100
=========================================

[Yadryara]

Табличка не для всех любителей мордоладонства

Мы с Демисом сегодня ещё по одному дротику метнули. И вот они в заявленной нотации.

Start_64                          Location  48  divisors  Valids Found
3ROG4OX7H3cXCtLifJYcUCUYxaw@Eh    1111111111111111111111      22    Na

AQK7IGkR9NQ1Gf900yv6GZTdkh        111111111111111111111       21    An
bW2p1imsGRcw7rB&CjUOBoionKzgxch   111111111111111111111       21    Vl
2z1IlbmMyyEhwWN@1W8g4c@kmz4Kp     1111111111111 11111111      21    An
3ziThLuHXPZlsC3IssprrJumxZbGh     11111111111 1111111111      21    De
4g&8IaO2VLOzyG03dm9A4kzaG@Mai     11111111111111 1111111      21    De
5dAUNCX@ZgzbsZwh@ibtS2Cse@vBi     11 1111111111111111111      21    De
63O5Y3gecECMY7mP8vydnJV7EKeRh     1111111111111111 11111      21    Vl
6jJ4BcAu3XvKwes4f@Cktsy6N&M&p     111 111111111111111111      21    An
6E04gmngJeEklXKft4VQ7A7CZ5aGp     11111111111 1111111111      21    An
6QkLs9OiVCCPiAVtbgz6jdSOnszWi     111111111111111 111111      21    De
7bUt5kNYVScSJ&0XYYIfiWM6bUByi     1 11111111111111111111      21    De
h8qnbrQuPQsCVH@Dm95WmPbUTjbFp     111 111111111111111111      21    An
m7LPET1a3ZAXwd&s7ueBuB83uySri     11111111111111111 1111      21    De
29J73OdwNKR02GyS8LIDPsl1fcw8Xh    111111111111111 111111      21    Vl
2cOrfRx&6mBRwfCvf3O3P7@g7exU0h    1111111111111111 11111      21    Vl

gris не желает ли потренироваться в расшифровке