Доброго времени суток.
Есть обобщение интегральной формулы Коши на случай неголоморфной функции класса

:
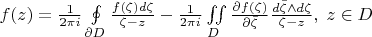
Я ее под разными названиями встречал. Не знаю какое общепринятое. Неважно.
Вопрос в том, почему вообще сходится второй интеграл? Производная перед дробью непрерывная по условию. Если перейти к другим переменным интегрирования

и
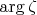
, то особенность в знаменателе все равно останется (тем более точка

произвольная в области

).
И второй вопрос, с которым я даже не знаю что делать. Допустим я хочу вычислить производную
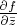
. Функция неголоморфная, должно что-то ненулевое получиться. Первый интеграл при таком дифференцировании ничего не даст. Под интегралом непрерывная функция, задана она на кривой

, область

ограниченная, по переменной

всё голоморфное. Вносим производную под интеграл, получаем нуль. Под второй интеграл производную, видимо, внести нельзя, но обоснование найти не могу. Есть теоремы, которые разрешают дифференцировать под знаком интеграла. Теорема, которая бы это запрещала, мне что-то на память не приходит.
Подскажите, пожалуйста. Просто хотя бы какие утверждения нужны. Правила читал, полного решения вопроса не прошу. Подсказки бы хватило. Заранее спасибо!