Школьная задача про космический корабль

[RikkiTan1]

Доброго времени суток!
Один мой знакомый по переписке, который сам по профессии врач, но который увлекается физикой, и который сейчас находится под надежной охраной государства, не может найти ошибку в своих рассуждениях в задаче, которую он сам и придумал.
Вот его рассуждения (привожу текст дословно со всеми кавычками).
Представим космический корабль цилиндрической формы, вращающийся для создания искусственной "силы тяжести". т.е. "центробежной силы".
Если взять радиус $r=10$м, то для создания во вращающейся системе отсчета цинтробежного ускорения $a_\text{цб}=10$ $\text{м}/c^2$
угловая скорость должна быть $w=1$ рад/с, линейная скорость "стенки" $v_\text{ст}=10$ м/с, правильно? Теперь представим, что нам удалось прыгнуть "вверх" (к оси вращения) с "начальной скоростью" $v_0=10$ м/с. Из элементарных геометрических построений выходит, что наше тело (в инерциальной системе отсчета) пройдет по хорде $\pi/2$ рад с постоянной скоростью $10\sqrt{2}\sim 14,2$м/с и через секунду "приземлится". За это время "земля"("стенка") сдвинется на 1 рад, т.е. на 10м. А $\pi/2$ рад - это у нас $\sim 15.7$ м. То есть "кориолисова сила" снесет нас аж на $5.7$ м в сторону. Но ведь при этом за секунду полета относительная "горизонтальная" (тангенциальная) скорость составит максимум (в "верхней точке" A ) всего $14.2-10=4.2$ м/с! Так что за 1 сек никак не может получиться $5.7$ м.

Может быть кто-нибудь видит, где в его рассуждения ошибка? Наверное это задача даже школьного уровня, но мною весь этот школьный материал физики и университетский материал теор. меха благополучно подзабыты.

[Theoristos]

Дам рассуждение побочное, но забавное.

Пусть у нас корабль вообще не вращается. Ровнёхонько 0 рад/с.
И космонавт так же прыгает вверх со скоростью 10 м/с.

Тогда за 2 с он пройдёт корабль насквозь и приземлится на противоположной, "верхней" стороне.
Путь от точки старта до приземления окружности равен $10\pi$ метров.
При этом для наблюдателя в этих двух точках "горизонтальная" скорость всё время равна 0. Как так?

Ну, а для наблюдателя на полпути по окружности, "справа", "горизонтальная" скорость на середине пути равна 10 м/с, что при умножении на 2с даёт 20 метров.

Так, что
1. Я бы всё-таки прояснил "интуитивно ясное" понимание этой "горизонтальной скорости".

Ибо, таракану, одновременно пущенному по окружности, чтоб сохранять одинаковую "высоту" с космонавтом нужно в начале бежать с бесконечной скоростью. И только на середине замедлиться до 10 м/с.

А таракан, который постоянно держит космонавта "в зените", вообще обречён оставаться на одном, стартовом месте. И в момент пересечения центра мгновенно телепортироваться в конечную точку.
А если, для снятия вырождения, корабль самую чуточку вращается. Так что космонавт движется чуть в сторону от центра - то такой таракан, держащий космонавта в зените, на середине пути должен бежать по стенке со скоростью гораздо выше 10 м/с, на отношение радиуса к расстоянию космонавта от центра.


2. Пути перемещения таки разные. Космонавт "срезает".

[RikkiTan1]

Большое спасибо за ваш ответ! Мой товарищ будет ему очень рад!

[EUgeneUS]

Вот с этого места начинается какая-то слабо понятная каша:

RikkiTan1 в сообщении #1696727 писал(а):

За это время "земля"("стенка")

Проще взять и зачеркнуть отсюда и до конца текста.

А поступать нужно более аккуратно. Вводя системы координат.
Например так:

1. Ведем систему координат в ИСО: точка отсчета - центр окружности, ось $Oy$ направлена вверх (по рисунку) и проходит через точку старта, ось $Oх$ направлена вправо (по рисунку).
Тогда в этой СК траектория, параметризированная временем:

$$x = 10t; y = 10(-1+t)$$

Вот тут нарисовано в Вольфраме для наглядности.

2. Далее перейдем в неИСО и построим там систему координат.
i. Пусть также $Oy$ проходит через точку старта, но теперь точка старта вращается вместе с окружностью.
За время $t$ система координат повернётся на угол $\varphi(t) = \omega t$
ii. пересчитаем координаты через поворот на угол $\varphi(t) = \omega t$:

$$x_1 = x \cos \varphi + y \sin \varphi = 10 (t \cos (t) + (-1+t) \sin(t))$$

$$y_1 = - x \sin \varphi + y \cos \varphi = 10 (- t \sin (t) + (-1+t) \cos(t))$$

Вот тут нарисовано в Вольфраме для наглядности

-- 08.08.2025, 18:00 --

И вот только теперь, если есть желание, можно дифференцировать $x_1, y_1$ по времени один или два раза и что-то с чем-то сравнивать.
А не рассуждать про мифическую "тангенциальную" скорость.

-- 08.08.2025, 18:16 --

Ещё, например, можно повернуть оси системы координат в неИСО, так чтобы траектория была симметричной относительно какой-нибудь оси.
Выглядеть это будет примерно вот так.
И уже в этой СК рассматривать перемещения, скорости и ускорения вдоль осей.

В общем, мораль сей басни такова: перед тем как рассуждать о перемещениях, скоростях и ускорениях вдоль осей системы координат, эту систему координат надо построить.

[RikkiTan1]

Большое спасибо! Отлично, то что нужно!

[Alex_O]

Доброго всем дня.
Можно тут небольшой вопрос задать? Только тут две ракеты:) . Гонщик и Эталон.
Летят с постоянным ускорением. В Гонщике, по стенкам ползают муравьи внутри трюма. Это внутреннее движение - не может изменять движение центра масс.

(Оффтоп)

Хитрый муравей (на потолке) сложил лапки и аккуратно - без рывка отсоединился от потолка. Масса Гонщика уменьшилась на массу муравья и он полетел быстрее. Через время $t$ - пол трюма "догнал" муравья, произошел обмен импульсом и скорость Гонщика равна Эталону, но он прошел больший путь и обогнал Эталон.

Когда муравей полз по стене трюма вверх - шагами - на каждом шаге Гонщик получал от муравья тормозной импульс и через время $t_{1}$ Гонщик "растерял" свое преимущество. Обе ракеты прилетят в пункт назначения по расписанию.

Но муравей оказался хитрее. На потолке была лебедка с тросом, муравей поднялся на потолок - на лебедке. Лебедка потратила энергию на работу против силы инерции муравья в неинерциальной системе отсчета. Сообщила муравью импульс.

Вопрос к физике лебедки.

Я, условно, "не вижу" "рывков". Я вижу силу натяжения троса лебедки и равномерное движение муравья в Системе Отсчета Гонщика.
Так же - лебедка - это внутренние силы - они не могут изменять движение центра масс. Условно - я вижу силы реакции в опоре лебедки и удивляюсь, что эта сила статичная. Отличается от "рывков" что создавал муравей- шагая по стене.
В учебных целях (изучить Python) я написал набор скриптов для численного решения ODE

Рис1. График энергии-импульса. Включая полезный граф - к.п.д, явно указывает на возможные ошибки, например, интегрирования. Например, тут не было учета затрат энергии на лебедку, что и отражается на графе к.п.д.

Полет ракеты (Гонщики и Эталона) разбит на ряд фаз, в каждой фазе используются различные ODE.


Рис.2 График перемещений, скоростей, ускорений.. В системе отсчета связанной с космодромом.

Пример простого скрипта

(Оффтоп)

start_fly ():
    """
    Фаза разгона ракеты и эталона на время Par.T_fly.
    Рассчитывается движение ракеты, груза и эталона, кинетическая энергия,
    импульсы и энергетический баланс системы. Позиция, скорость и ускорение
    центра масс Body также сохраняются и печатаются.
    """
    global current_phase
    current_phase = 'start_fly'

    dt = 1.0  # шаг интегрирования в секундах

    # --- начальные позиции и скорости ---
    read_data (r)        
    
    # --- массы и ускорения ---
    Body.Massa = Rocket.Massa + Cargo.Massa
    Body.Massa_cur = Rocket.Massa + Cargo.Massa
    
    r.a_rocket_x = Force.Thrust / Body.Massa   # ускорение ракеты + груза
    r.a_cargo_x  = r.a_rocket_x                # груз движется вместе с ракетой
    r.a_model_x  = Force.Thrust / Model.Massa  # ускорение эталона

    # --- временные счетчики ---
    Time = 0
    Time_run = Par.Timer

    # --- интегрирование движения ---
    while (Time - Time_run) <= Par.T_fly - dt:

        # сохраняем старые значения для интеграла работы
        save_old () 

        # --- интеграл движения (положение и скорость) ---
        Calck_int_motion(dt)        

        Time += dt
        Par.Timer += dt

        # --- сохраняем рассчитанные ускорения, скорости и позиции ---
        save_data (r)        
        # --- Центр масс Body ---
        update_body_cm ()
        # Body.Move  = (Rocket.Massa * Rocket.Move + Cargo.Massa * Cargo.Move) / Body.Massa
        # Body.Speed = (Rocket.Massa * Rocket.Speed + Cargo.Massa * Cargo.Speed) / Body.Massa
        # Body.Boost = (Rocket.Massa * Rocket.Boost + Cargo.Massa * Cargo.Boost) / Body.Massa

        # --- энергетика и импульсы ---
        ledger_update(dt, F_link=None, v_rel=None)  # работа и импульсы за шаг
        energy_and_pulse_update()                   # импульсы и энергии, баланс
        save_to_history()                           # сохраняем данные для графиков

        # --- печать текущего состояния для контроля ---
        # to_print_in_faza()
    end_phase(Par.Timer -r.t_faza_run) 

def Calck_int_motion(dt = 0.0): # расчет интегралов движения
    r.p_rocket_x += r.v_rocket_x * dt + 0.5 * r.a_rocket_x * dt**2
    r.v_rocket_x += r.a_rocket_x * dt

    r.p_cargo_x  += r.v_cargo_x * dt + r.a_cargo_x * dt * dt / 2 
    r.v_cargo_x  += r.a_cargo_x * dt

    r.p_model_x += r.v_model_x * dt + 0.5 * r.a_model_x * dt**2
    r.v_model_x += r.a_model_x * dt

Согласно графикам, Гонщик проиграл Эталону, так как в фазе лебедка - груз совершил ускоренное движение на лебедке в неинерциальной системе отсчета.

Но если , рывки лебедки исключены, силы натяжения троса компенсируется в опоре, лебедка как абсолютно внутренние силы - то Гонщик прилетит к финишу раньше.

Рис 3. Лебедка равномерно, с момента включения переместила груз на потолок.
ПО показывает нарушение баланса импульса внутри фазы (это видно на графе наглядно).
---
Вопрос по "лебедке и учета центра масс. Образно - в начале, груз (муравей) сидел на потолке - в центре масс. Упал, вернулся на лебедке. В процессе падения груза (внутри трюма) система физически разделилась на две абсолютно независимые подсистемы (трения нет) Корпус ракеты Гонщика и Груз. Ракета под воздействием тяги мотора - совершает рывок. Ее центр масс улетает вперед - а лебедка - "просто" возвращает груз в исходное положение - в точку центра масс. Но хорошо видно, что центр масс (с учетом полета груза) движется так же, как ЦМ Эталона.

(Оффтоп)

сразу отмечу, что если добавить фазу - разгон груза лебедкой до начальной скорости - это фатально тормозит Гонщика и он проиграет гонку.

Не уверен, что пост не содержит ошибок правил форума, укажите мне ошибки, если они есть.

[realeugene]

Alex_O в сообщении #1710330 писал(а):

Летят с постоянным ускорением.

Alex_O в сообщении #1710330 писал(а):

Масса Гонщика уменьшилась на массу муравья и он полетел быстрее.

Эти две фразы противоречат друг другу.

Кажется, вы просто сами запутались. Пользуйтесь только инерциальными системами отсчёта если получаете кажущиеся противоречия.

[Alex_O]

realeugene в сообщении #1710340 писал(а):

Alex_O в сообщении #1710330 писал(а):

Летят с постоянным ускорением.

Alex_O в сообщении #1710330 писал(а):

Масса Гонщика уменьшилась на массу муравья и он полетел быстрее.

Эти две фразы противоречат друг другу.

Кажется, вы просто сами запутались. Пользуйтесь только инерциальными системами отсчёта если получаете кажущиеся противоречия.

Летят с постоянным ускорением. включенным двигателем. Извините за неточность формулировки, я хотел сделать максимально корректное описание задачи.

Например, двигатель Гонщика можно дросселировать (в разное время, в нужной фазе) и я, как то, даже не понял результаты расчетов и что, вообще, можно ожидать, если учесть скорость изменения ускорения (рывок, jerk, третья производная от координаты).

(Оффтоп)

def Calck_int_motion_with_jerk(dt=0.0):
    """
    Интегратор с учетом рывка для ракеты и груза
    Эталон - без рывка (постоянное ускорение)
    """
    global prev_a_rocket, prev_a_cargo
    
    # Рывок только для ракеты и груза
    r.j_rocket = (r.a_rocket_x - prev_a_rocket) / dt if dt > 0 else 0
    r.j_cargo = (r.a_cargo_x - prev_a_cargo) / dt if dt > 0 else 0
    
    # Ракета и груз - с рывком
    r.p_rocket_x += r.v_rocket_x * dt + 0.5 * r.a_rocket_x * dt**2 + (1/6) * r.j_rocket * dt**3
    r.v_rocket_x += r.a_rocket_x * dt + 0.5 * r.j_rocket * dt**2
    
    r.p_cargo_x += r.v_cargo_x * dt + 0.5 * r.a_cargo_x * dt**2 + (1/6) * r.j_cargo * dt**3
    r.v_cargo_x += r.a_cargo_x * dt + 0.5 * r.j_cargo * dt**2
    
    # Эталон - без рывка (равноускоренное движение)
    r.p_model_x += r.v_model_x * dt + 0.5 * r.a_model_x * dt**2
    r.v_model_x += r.a_model_x * dt
    
    # Сохраняем для следующего шага
    prev_a_rocket = r.a_rocket_x
    prev_a_cargo = r.a_cargo_x

Вопрос не много сложнее, чем кажется. Заменим лебедку .. воздушным шаром. Что будет? Можно обострить - пусть корпус ракеты Гонщика, условно, мягкий, как мыльный пузырь. Энергия лебедки, через реакции в опорах как то диссипирует в стенках..

Или

В статье J Wisdom · 2002 — Swimming in Space-Time. Jack Wisdom. AI Memo 2002-017. November 2002.
Обсуждается плавание в искривленном пространстве-времени за счет внутренних сил.

Цитата:

Cyclic changes in the shape of a quasi-rigid body on a curved manifold can lead to net translation and/or rotation of the body in the manifold. Presuming space-time is a curved manifold as portrayed bygeneral relativity, translation in space can be accomplished simply by cyclic changes in the shape of a body, without any thrust or external forces.

Если предположить, что пространство-время является искривлённым многообразием, как это описывается общей теорией относительности, движение в пространстве может осуществляться исключительно циклическими изменениями формы тела, без какой-либо тяги или внешних сил.

(Пример полезного анализа статьи тут)
Цитаты из статьи:

Цитата:

Для объекта метрового размера, совершающего метровые деформации на поверхности Земли, смещение составляет порядка $10^{-23}$ метра.
..
Цель состоит в том, чтобы определить, возможно ли плавание в пространстве-времени. Поэтому достаточно рассмотреть специальную ориентацию тела. Если ось тела ориентирована радиально от центральной массы, то симметрия геометрии Шварцшильда и трёхкратная симметрия пловца гарантируют, что любое перемещение, вызванное циклической деформацией, будет происходить только в радиальном направлении
..
Смещение будет пропорционально квадрату отношения размера объекта к радиусу кривизны многообразия. Для геометрии Шварцшильда компоненты тензора кривизны Римана пропорциональны GM/(c2r3), что можно рассматривать как величину, обратную квадрату эффективного радиуса кривизны.

Формула (74) в конце статьи

$$\Delta r = -3m_0m_1/(m_0 +3m_1)^2 l^2 \frac{GM}{c^2r^3} \sin\alpha \Delta l \Delta \alpha$$

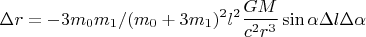
характерно содержит величину компоненты тензора кривизны Римана в метрике Шварцшильда: $ R \sim \frac{GM}{c^2r^3} $

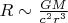
Формула описывает радиальное смещение («плавание») квази-жёсткого тела в искривлённом пространстве-времени Шварцшильда за счёт циклических изменений формы тела.

(Оффтоп)

Массовый множитель

$$ -3m_0m_1/(m_0 +3m_1)^2 l^2 $$

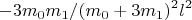
Это безразмерный коэффициент, зависящий от распределения масс.
Максимум достигается при $m_0=3m_1$
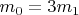
Геометрический размер тела

$$l^2$$

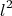
$l$ — собственная длина стержней в локальной системе отсчёта.
(см рис.3 статьи)
Квадрат длины отражает то, что эффект зависит от площади, "заметаемой" в пространстве параметров деформации .
Кривизна пространства-времени

$$\frac{GM}{c^2r^3}$$

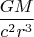
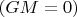
Эффект плавания пропорционален кривизне: на плоскости $(GM=0) $ эффекта нет.

Параметры деформации

$$\sin\alpha \Delta l \Delta \alpha$$

Физическая интерпретация
Механизм: циклическое изменение $l(t)$ и $\alpha(t)$ создаёт нетто-смещение в радиальном направлении благодаря кривизне пространства-времени.
Аналогия: как жук на сфере может двигаться, меняя форму, так и здесь тело «плывёт» без внешних сил, используя геометрическую фазу в искривлённом пространстве-времени.
Масштаб эффекта:
Для $ l\sim 1\text{ м}, r\sim R\oplus,\Delta l\sim l, \Delta\alpha\sim 1$

$$ \Delta r\sim 10^{-23}\text{ м} $$

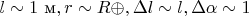
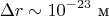
Чрезвычайно мал из-за слабой кривизны у Земли

Что это значит?
Сделана попытка заменить слабый фон кривизны пространства на более сильный фон - внешней силы от реактивной тяги ракеты.

Или так можно определить:
Wisdom использует гравитационную кривизну, а здесь используется реактивная тяга, которая создаёт искусственное поле инерции на десятки порядков сильнее.

Для разминки - в спойлере небольшой результат попытки понять сабж лучше. Опуская делали ( и расчеты) - тезисно.

(Оффтоп)

Тезисно: "Плавание в искривлённом пространстве-времени и его электромагнитные аналоги"
(Обсуждение на основе AI Memo 2002-017 Дж. Уиздома)

1. Гравитационное "плавание" по Уиздому

Принцип: Циклические изменения формы квази-жёсткого тела в искривлённом пространстве-времени (ОТО) приводят к поступательному смещению центра масс без реактивного импульса. Эффект является геометрической фазой (аналог фазы Берри).

Формула (для метрики Шварцшильда):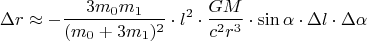

$$\Delta r \approx -\frac{3m_0 m_1}{(m_0+3m_1)^2} \cdot l^2 \cdot \frac{GM}{c^2 r^3} \cdot \sin\alpha \cdot \Delta l \cdot \Delta\alpha$$

где $l$ – характерный размер тела, $\alpha$ – угол деформации.

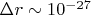
Проблема: Эффект ничтожно мал для земных условий ($\Delta r \sim 10^{-27}$ м за цикл).

2. Попытки усиления эффекта

2.1. Частотный "допинг"
Увеличение частоты циклов деформации $\nu$ линейно увеличивает среднюю скорость дрейфа:

$$\langle v \rangle = \Delta r \cdot \nu$$

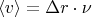
Однако, сам эффект за цикл $\Delta r$ от скорости не зависит. Чисто геометрическая фаза.

2.2. "Брасс" по Белецкому в поле Ньютона
Рассмотрена модель "гантели" в сильном гравитационном поле (апогей/перигей).
• Сжатие/растяжение плеч гантели в разных точках орбиты приводит к изменению орбитальных элементов.
• Аналог плавания: За счёт разности гравитационных сил в точках с разным потенциалом, циклическая деформация позволяет совершать работу против поля.
• Эффект значительно превосходит "плавание по Уиздому" в слабых полях, так как использует силу самого гравитационного поля, а не только кривизну.

3. Переход к электромагнитным "искривителям"

Ввиду малости гравитационного эффекта, предложено использовать электромагнитные поля, где силы на порядки больше.

3.1. Принцип ЭМ-искривителя
• Космодром создаёт стационарное магнитное поле $B_{\text{косм}}$.
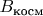
• Корабль (КА) имеет замкнутый сверхпроводящий контур с током $I_{\text{КА}}$.
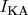
• Сила Ампера создаёт ускорение:

$$F = I_{\text{КА}} \cdot L \cdot B_{\text{косм}} \quad \Rightarrow \quad a = F / m_{\text{КА}}$$

• Ключевое отличие от рельсотрона: Бесконтактное ускорение, нет эрозии "ствола".

3.2. Сравнительная оценка систем



3.3. Меркурий как идеальный ЭМ-космодром
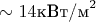
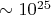
• Энергия: Высокий солнечный поток ($\sim 14 \text{кВт/м}^2$) позволяет аккумулировать до $\sim 10^{25}$ Дж/год.
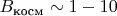
• Усиление поля: Возможно создание глобальной сверхпроводящей сети на поверхности для генерации гигантского магнитного поля ($B_{\text{косм}} \sim 1-10$ Тл).
• "Допинг" от Солнца: Слабое фоновое магнитное поле Солнца и солнечный ветер могут использоваться для дополнительного ускорения КА с магнитным парусом после старта.
• Стабилизация отдачей: Гравитация Солнца позволяет использовать его для гравитационных манёвров по компенсации отдачи космодрома.

4. Вывод
• Гравитационное "плавание" (Уиздом) – фундаментальный, но практически ничтожный эффект.
• "Плавание" в сильных полях (Белецкий) – более мощный механизм, использующий градиент потенциала.
• ЭМ-искривитель – наиболее практичный и мощный аналог, переносящий принцип геометрической фазы в область электромагнетизма.
• Меркурий является идеальной платформой для ЭМ-космодрома межзвёздного класса, объединяя энергию Солнца, его гравитацию для стабилизации и возможность создания сверхсильных искусственных полей.

Заключение: Переход от гравитационных "искривителей" к электромагнитным открывает путь к созданию орбитальных катапульт, способных разгонять КА до релятивистских скоростей в масштабах Солнечной системы. Это пример мышления цивилизации II типа по Кардашёву.

Пока готовил этот пост (с утра!) возникло предположение.
Что Гонщик - в нем есть деформации на фоне сильного поля (инерции/внешней силы) кажется отличается от выше описанных "деформаторов" тем, что нет полезной "кривизны". Или вектор деформации - по вектору тяги - по "силовым линиям " а не перепендикулярно.

Поле сил есть? есть. Деформации есть? Должно полететь. Что не хватает?

[amon]

Alex_O в сообщении #1710330 писал(а):

Это внутреннее движение - не может изменять движение центра масс.

Центра масс - не может, а положение переднего конца ракеты - запросто. Если убрать все лишнее, и оставить массу $m$ у заднего конца ракеты массы $M$ (неподвижной), то при передвижении этой массы в нос ракеты, ракета сдвинется назад так, чтобы центр масс остался на месте. И не важно, переползла эта масса перебирая лапками, или ее протащила лебедка. Если ракета движется с ускорением, значит к ней приложена внешняя сила, и надо аккуратно учесть, что Ваш муравей стукнется о дно, а лебедка должна его ускорить прежде чем она начнет двигать его с постоянной скоростью. Поэтому "не видеть рывков" и считать, что трос лебедки равномерно движется - лучший способ провраться.

[realeugene]

Alex_O в сообщении #1710385 писал(а):

Вопрос не много сложнее, чем кажется.

Вопрос вообще не понятен, так как не вижу, где он сформулирован. Вы наткнулись на противоречие и ищете ошибку в своих расчётах? У вас очень много текста, не понятно, зачем?

И это разве не совершенно новая тема?

[Alex_O]

amon в сообщении #1710386 писал(а):

Alex_O в сообщении #1710330 писал(а):

Это внутреннее движение - не может изменять движение центра масс.

Центра масс - не может, а положение переднего конца ракеты - запросто. Если убрать все лишнее, и оставить массу $m$ у заднего конца ракеты массы $M$ (неподвижной), то при передвижении этой массы в нос ракеты, ракета сдвинется назад так, чтобы центр масс остался на месте. И не важно, переползла эта масса перебирая лапками, или ее протащила лебедка. Если ракета движется с ускорением, значит к ней приложена внешняя сила, и надо аккуратно учесть, что Ваш муравей стукнется о дно, а лебедка должна его ускорить прежде чем она начнет двигать его с постоянной скоростью. Поэтому "не видеть рывков" и считать, что трос лебедки равномерно движется - лучший способ провраться.

Благодарю.

Вы мне очень сильно помогли. Лебедка тут не причем. Все дело в реактивной струе. Она должна мешать Гонщику тормозиться при падение груза на корму. Третья сила. Задача трех тел. Не знаю пока как это можно учесть - кажется можно постулировать - что тяга мотора ракеты явно увеличивается при падении груза на пол. Ниже покажу концепт типа "гравитационный якорь".

-- 24.11.2025, 08:44 --

realeugene в сообщении #1710387 писал(а):

Alex_O в сообщении #1710385 писал(а):

Вопрос не много сложнее, чем кажется.

Вопрос вообще не понятен, так как не вижу, где он сформулирован. Вы наткнулись на противоречие и ищете ошибку в своих расчётах? У вас очень много текста, не понятно, зачем?

И это разве не совершенно новая тема?

Я решаю задачу трех тел. Случайно получилось. Солнце, астероид (астер), прыгун.
Наивный вопрос - можно ли уронить астер, если на него сбросить прыгающий мяч. Все сразу отвечают - нельзя. Но я случайно посмотрел сим трех тел (three body problem) и был удивлен .. Три звезды в учебном симе летали по одной орбите - и через время совершили головокружительный финт.

Быстрые оценки на реальном примере (Солнце, орбита Земли, астер массой миллиард тонн, разумный прыгун массой 1000 тонн). Сила притяжения Солнца. .
Если прыгун скачет в гравполе астера по баллистике - период осцилляций на уровне 2000 секунд. Если эффект и есть - потребуется "миллион лет" .

Поставим на астер - механический резонатор ("сарай") . Прыгун скачет внутри сарая с периодом условно 2 секунды. Пусть астер свободно падает к Солнцу. Это для упрощения - нет учета орбитальных моментов.. Это как лифт Эйнштейна (похоже), но есть вопрос. Что будет, если под лифт положить ..палец наблюдателя...

Другим словами - прыжки прыгуна в задаче трех тел - все расчета балансов следует вести для трех тел. Толкая астер к Солнцу - мы получаем "допинг" от Силы Солнца, и пытаемся сдвинуть Солнце - при отскоке (удар в потолок).

Тема получила название - гравитационный якорь. В ходе обсуждения принято решение разработать ПО для моделирование с учетом возможных нюансов (задача об ударе клюшки для гольфа об мяч для гольфа - известна и характерна качеством проработки мелких деталей, включая видеосъемку быстрой камерой) .

Случайно, был найден пример Гонщика с падающими грузами. Как некий более физичный аналог. Вообще то - надо внести в систему гравитационный якорь (гравякорь), но вначале думалось что реактивная сила - как некий аналог якоря.
Сегодня , утром.. возникла идея об учете физики реактивной струи - как третьей силы. (можно показать результаты исследования в NASA и других - где была модель реактивного мотора с эжекторами (установлены после сопла). Видели усиление тяги мотора. )

==
Предыдущий пост был немного избыточен - приношу извинения - я хотел немного показать качество. С новой темой - я не уверен. Моделирование Гонщика показало отрицательный результат - но !! выход на dxdy с вопросом - принес неожиданный и крайне полезный результат. Мои благодарности аудитории!!

[realeugene]

Alex_O в сообщении #1710436 писал(а):

Я решаю задачу трех тел. Случайно получилось. Солнце, астероид (астер), прыгун.
Наивный вопрос - можно ли уронить астер, если на него сбросить прыгающий мяч. Все сразу отвечают - нельзя. Но я случайно посмотрел сим трех тел (three body problem) и был удивлен .. Три звезды в учебном симе летали по одной орбите - и через время совершили головокружительный финт.

Ах, вот оно в чём дело...

Задача трёх тел сложна когда три тела примерно одинаковой массы. Когда летает астероид гораздо меньшей массы, чем масса Солнца (любой астероид и даже Юпитер имеют массу, гораздо меньшую массы Солнца) центр масс системы гарантированно всегда находится очень близко к геометрическому центру Солнца, и никаких головокружительных кульбитов Солнце совершать не может. Приближение центральносимметричного гравитационного поля Ньютона работает для всех летающих вокруг планет и, тем более, астероидов почти идеально. И вам не нужно даже притрагиваться к ОТО как к чему-то мистическому. Так что у вас летает ракета по эллиптической орбите, и вам нужно оценить, насколько сильно и быстро можно изменить орбиту за счёт внутренних движений. Заведомо всё будет изменяться очень медленно, так что оценивайте возможные малые возмущения.

Законы сохранения в задаче трёх тел при этом никуда не деваются. Суммарные импульс и момент импульса этих кувыркающихся звёзд в любой ИСО сохраняются точно. Как и вашей ракеты с космонавтом внутри, летающей вокруг Солнца. Попытайтесь оценить на сколько изменятся параметры эллипса за один оборот по эллипсу, если у вас летает гантеля из двух масс, длину которой вы можете быстро изменить в апогелии и перигелии при помощи внутреннего мотора. Это будет малая поправка к эллипсу.

Рассматривать ракетные двигатели совершенно точно не нужно, так как если у вас вылетает струя газа, это уже не задача трёх тел, которую вы хотите рассмотреть.

[Alex_O]

realeugene в сообщении #1710450 писал(а):

Alex_O в сообщении #1710436 писал(а):

Я решаю задачу трех тел. Случайно получилось. Солнце, астероид (астер), прыгун.
Наивный вопрос - можно ли уронить астер, если на него сбросить прыгающий мяч. Все сразу отвечают - нельзя. Но я случайно посмотрел сим трех тел (three body problem) и был удивлен .. Три звезды в учебном симе летали по одной орбите - и через время совершили головокружительный финт.

Ах, вот оно в чём дело...

Задача трёх тел сложна когда три тела примерно одинаковой массы. Когда летает астероид гораздо меньшей массы, чем масса Солнца (любой астероид и даже Юпитер имеют массу, гораздо меньшую массы Солнца) центр масс системы гарантированно всегда находится очень близко к геометрическому центру Солнца, и никаких головокружительных кульбитов Солнце совершать не может. Приближение центральносимметричного гравитационного поля Ньютона работает для всех летающих вокруг планет и, тем более, астероидов почти идеально. И вам не нужно даже притрагиваться к ОТО как к чему-то мистическому. Так что у вас летает ракета по эллиптической орбите, и вам нужно оценить, насколько сильно и быстро можно изменить орбиту за счёт внутренних движений. Заведомо всё будет изменяться очень медленно, так что оценивайте возможные малые возмущения.

Законы сохранения в задаче трёх тел при этом никуда не деваются. Суммарные импульс и момент импульса этих кувыркающихся звёзд в любой ИСО сохраняются точно. Как и вашей ракеты с космонавтом внутри, летающей вокруг Солнца. Попытайтесь оценить на сколько изменятся параметры эллипса за один оборот по эллипсу, если у вас летает гантеля из двух масс, длину которой вы можете быстро изменить в апогелии и перигелии при помощи внутреннего мотора. Это будет малая поправка к эллипсу.

Рассматривать ракетные двигатели совершенно точно не нужно, так как если у вас вылетает струя газа, это уже не задача трёх тел, которую вы хотите рассмотреть.

Отлично.

Задача трех тел - тут в контексте как источник идеи, конечно. Ракеты - как идея проверки общей физики. Если прыгун может уронить астер, используя Солнце как гравитационный якорь - за счет асимметрии на уровне астероида, то возникала идея, что Реактивный мотор может быть полезен лучше.

Подтвердилось первыми расчетами. Я пока не нашел практичных аналогов (что то из области - что тяга мотора при торможении больше чем при разгоне, а пробные оценки некой жесткость газовой подушки под кормой ракеты (или в зоне сопла) могут сойтись на уровне 1% от тяги. Детали не важны - можно сходу показать концепт вброса в резонатор порций энергии от бортового источника (с условным к.п.д 99%) и коротким дросселированием тяги в разных фазах. Конечный результат может показать полезное (прирост ПН или экономию топлива). Отдельно можно изучать более быстрые "прыгуны" , например, электромагнитные. Как курьез или напротив, смело - можно показать идею коррекции МКС за счет прыгающих космонавтов (физические упражнения). Есть пример быстрого расчета с красивыми итогами - экономия топлива, затрат и согласие с медициной.

Рад показать результат учета "третьей силы" в ракете.
В спойлере код цикла - по фазам.

(Оффтоп)

    for cycle in range(1, num_cycles + 1):
        print(" =============== прыжки  =========================")

        print("Полет груза вниз ")
        push_faza()
        to_print()
        
        print("brake_spring - Торможение грузов на пружине с учетом газового тормоза")
        brake_spring()        
        to_print()
       
        print("brake_spring_up - разгон груза на пружине ")
        brake_spring_up()        
        to_print()

        # Par.Flag_Print = "Yes"    
        print("Лебедка тянет груз вперед c постоянной скоростью")
        winch()
        to_print()

        print("Лебедка - торможение за счет обмена импульсом")
        stuck()       # торможение за счет обмена импульсом

        print(f" ЦИКЛ {cycle} ЗАВЕРШЕН")

В фаза - торможение груза на полу пружиной - добавилась поправка от газовой струи. Это - просто внешняя сила. После нее - к.п.д просто больше 100%.
вот фрагмент кода ODE

    # 24/11/25 Третья сила  - реактивная струя мешает тормозить Гонщика
    # Ускорения с учётом "газового амортизатора"
    # СТРУЯ СОЗДАЁТ ДОПОЛНИТЕЛЬНОЕ СОПРОТИВЛЕНИЕ ТОРМОЖЕНИЮ
    r.a_rocket_x = (Force.Thrust - Force.Friction + Force.Jet_damping)/Rocket.Massa  
    r.a_cargo_x = Force.Friction / Cargo.Massa    
    while r.v_rocket_x - r.v_cargo_x > 0.0001:  # до выравнивания скоростей
        # сохраняем старые значения для интеграла работы
        save_old()
        # Интегрирование
        Calck_int_motion(dt)

вот это $+Force.Jet_damping =$ - ключ к успеху.


На графе скоростей - синяя и зеленая линия пересекаются в точке что выше красного пунктира. Это и есть результат асимметрии.

к.п.д больше 100% так как термин - вклад третьей силы не учтен в балансе. Для наглядности.

Эффект накапливается на каждом цикле - прогрессивно.

Рис 3 - 3-и цикла.


Рис 4 - 20 цикла. В центре внизу - граф преимущества (в метрах).

Как то так, даже если идея газового тормоза сомнительна - можно изучить идеи оптимизации дизайна сопла. Например, с локальным уширением. А любой импульсный мотор может быть улучшен за счет инсталляции прыгунов и переменного дросселирования.
(Образно, ракета летит на Марс и везет в трюме ПН для марсиан. Это балласт, что может быть активным участником реактивного движения).

[realeugene]

Alex_O в сообщении #1710693 писал(а):

В спойлере код цикла - по фазам.

Не, искать ошибки в вашем коде я не буду.

Alex_O в сообщении #1710693 писал(а):

Ракеты - как идея проверки общей физики.

Физика работает, её проверять не нужно

В одномерном случае, в котором вы что-то считаете, невозможность ускориться за счёт внутренних движений - это закон физики. Если вы насчитали что-то иное - у вас в программе ошибка.

При вращении вокруг Солнца может быть за миллиард лет вы и сожмёте эллипс достаточно сильно. Каждый оборот аппарата вокруг Солнца порядка года, быстро не получится, так что опять же идея бесплодна.

[Alex_O]

realeugene в сообщении #1710694 писал(а):

Alex_O в сообщении #1710693 писал(а):

В спойлере код цикла - по фазам.

Не, искать ошибки в вашем коде я не буду.

В одномерном случае, в котором вы что-то считаете, невозможность ускориться за счёт внутренних движений - это закон физики. Если вы насчитали что-то иное - у вас в программе ошибка.

Это даже школьнику понятно. Я прошу извинения, я наверно плохо формализовал.
Уточняю.

Выброшенная реактивная масса, в ближней зоне реактивного мотора представляет собой некоторое облако газа. Пробный расчет проведен с учетом силы действия со стороны облака газа на ракету в момент падения груза.