квантовое «измерение» в момент создания запутанной пары

[Cos(x-pi/2)]

naskamejke в сообщении #1710310 писал(а):

они экспериментально получили интерференцию для фотона 1, а не 2

В статье обсуждается всё-таки интерференция для фотона 2:

Zeilinger писал(а):

Photon 2 enters a double-slit assembly and photon 1 is registered by the Heisenberg detector arranged behind the Heisenberg lens. If the Heisenberg detector is placed in the focal plane of the lens, it projects the state of the second photon into a momentum eigenstate which cannot reveal any position information and hence no information about slit passage. Therefore, in coincidence with a registration of photon 1 in the focal plane, photon 2 exhibits an interference pattern.

Счёт совпадений да, принципиально важен.

Автор не описал подробно этот эксперимент и его теорию (и работу Допфер не удаётся скачать, да она и не на английском языке.) Однако понятно, что подробное количественное изложение здесь должно быть сложным - пришлось бы описывать распределение в пространстве и свойства когерентности световых пучков, притом до щелей и после, до линзы и после. По-видимому, автор решил не утяжелять громоздкими формулами эту в общем-то научно-популярную статью.

Попробую написать в упрощённом виде, как я понимаю этот эксперимент. (Хотя в соседней теме я выступал против упрощенчества, поскольку оно легко превращается во враньё, но этот сюжет понять и изложить без выкидывания деталей у меня не получается. Буду надеяться, что для понимания принципиальной стороны дела "сойдёт и так" :)

[naskamejke]

Cos(x-pi/2) в сообщении #1710337 писал(а):

В статье обсуждается всё-таки интерференция для фотона 2

Ну да, обсуждается интерференция для фотона 2, а потом раз - и приводятся данные для фотона 1 - рисунок 4. И это не опечатка, в тексте это специально подчеркивается, как удивительный факт.
А по-моему это как раз не удивительно. Я понимаю так. Вот зарегистрирован фотон 1 в фокальной плоскости в определенном месте. Это означает определенный импульс фотона 1, определенное направление. Фотоны скореллированы (и не обязательно как запутанная пара, смесь тоже подошла бы), т. е. фотон 2 тоже имеет определенное направление. Но место его регистрации неизменно, и будет он зарегистрирован или нет (точнее сколько фотонов будет зарегистрировано при потоке) зависит от интерференционной картины для данного направления движения фотонов. Что и создает впечатление интерференции для фотона 1. Вообще-то рисунок 4 может сбить с толку. По вертикальной оси написано количество условных отсчетов фотона 1, смысл - количество совпадений - когда регистрируются оба фотона, но я сначала этого не понял. Вот мне так кажется.

[realeugene]

naskamejke в сообщении #1710358 писал(а):

Фотоны скореллированы (и не обязательно как запутанная пара, смесь тоже подошла бы), т. е. фотон 2 тоже имеет определенное направление.

Чуть дальше в статье написано, что очевидно, что просто статистическая смесь попарно скоррелированных фотонов не может привести к подобной идеальной модуляции в интерференционной картине первого фотона. Честно говоря, мне это тоже не вполне очевидно, но очевидно, что в этом можно поверить автору статьи.

На основе этой установки можно придумать воображаемый эксперимент, в котором оба детектора на самом деле CCD матрицы, регистрирующие момент и положение прихода каждого фотона в своей плоскости. Тогда каждая матрица будет регистрировать какие-то распределения приходящих фотонов как отдельные вспышки в отдельных точках матриц в случайные моменты времени. Эти распределения положения каждого фотона будут гладкими без интерференционных максимумов и минимумов, так как каждый фотон получается в паре со спутанным с ним фотоном, без разницы, регистрируется спутанный фотон или нет. Если отобрать совпадающие по времени вспышки в обоих матрицах, соответствующие спутанным парам фотонов, распределения в каждой матрице всё ещё будут гладкими без интерференционных пиков и минимумов. Но если отобрать из этих пар те пары, в которых один фотон будет прилетать в определённый элемент одной матрицы, то для второго фотона пары будет наблюдаться интерференционная картина на второй матрице. Но положение этих интерференционных максимумов будет сдвигаться в зависимости от того, по какому именно условию положения первого фотона мы отобрали эти совпадающие во времени пары, так что при осреднении по этому положению-условию первого фотона интерференционная картина для другого фотона будет исчезать. (Здесь слова первый и второй фотон отличаются от обозначений статьи, на самом деле, фотоны симметричны).

[chislo_avogadro]

Cos(x-pi/2) в сообщении #1710337 писал(а):

Автор не описал подробно этот эксперимент и его теорию (и работу Допфер не удаётся скачать, да она и не на английском языке.)

Да, это диссертация на немецком, под руководством, как можно догадаться, Антона Цайлингера. Там неясно, проводился ли этот эксперимент в рамках диссертации или это лишь рассуждения по поводу. Но есть ссылка на проводившийся эксперимент. Там об отложенном выборе речи, однако, нет.

[realeugene]

chislo_avogadro в сообщении #1710380 писал(а):

Там об отложенном выборе речи, однако, нет.

Отложенным выбором называют селекцию статистики результатов пар измерений по какому-то критерию? Когда у нас измеряются запутанные частицы, интерференция проявляется в некоторым образом отобранной совместной статистике. Измерения можно провести независимо, пометив их некоторым образом заранее синхронизированным временем, и отобрать нужную статистику сильно позже, увидев в статистике необычные для классического мира корреляции. Классическая электронная схема совпадения очевидно для этого не нужна.

[Cos(x-pi/2)]

chislo_avogadro, большое спасибо за статьи (я их только сейчас увидел, ещё не читал, позже попробую в них разобраться).

Коллеги, похоже в общем вы всё верно пишете. А я, пока ваших сообщений не видел, писал "простыню", наверное теперь неактуальную:

(Моя попытка поразмышлять об опыте Цайлингера и Допфер)

В самом общем виде (в том числе и безотносительно к показанному на рис.3эксперименту из статьи A. Zeilinger, см. ссылку в сообщении chislo_avogadro) "запутанное по импульсу" состояние $|\Psi\rangle$ пары частиц 1 и 2 можно записать так:

$$|\Psi\rangle=\sum_{\mathbf{p}}\sum_{\mathbf{q}}C_{\mathbf{p},\mathbf{q}}\,|\mathbf{p}\rangle_1\otimes|\mathbf{q}\rangle_2$$

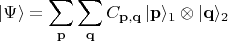
В контексте нашего сюжета это выражение расшифровывается вот как. В постановке опыта, который описывается этим выражением, аппаратура обеспечивает измерение вектора импульса, например, частицы 1. Источник частиц обеспечивает корреляцию результатов измерений, притом разную в разных постановках опыта. 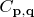Когда измеряется импульс частицы 1, корреляция такая: если у частицы 1 обнаружился импульс $\mathbf{p}$ (конкретный из множества возможных векторов импульса), то у частицы 2 может с заданной амплитудой вероятности $C_{\mathbf{p},\mathbf{q}}$ обнаружиться импульс $\mathbf{q}$ (один из множества возможных). 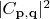$|C_{\mathbf{p},\mathbf{q}}|^2$ есть вероятность обнаружить у частицы 1 данный импульс $\mathbf{p}$ и при этом у частицы 2 обнаружить импульс $\mathbf{q}.$

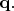
Знак тензорного произведения $\otimes$ читается как слова "и при этом". По алгебраическим свойствам знак $\otimes$ это операция умножения, т.е. если сомножители будут иметь вид скобок с линейными комбинациями векторов состояния, то скобки можно будет раскрыть по обычным правилам алгебры.

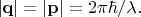
В опыте Zeilinger с парами фотонов длина волны $\lambda$ в пучках света 1 и 2 одинаковая, притом фиксированная. Значит, величина импульса у всех фотонов одинаковая: $|\mathbf{q}|=|\mathbf{p}|=2\pi\hbar/\lambda.$ От пары к паре могут флуктуировать только направления вылета фотонов 1 и 2 из кристалла-источника, но лишь так, что суммарный вектор импульса фотонов в каждой паре будет одинаковым для всех пар.

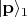
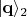
Поэтому будем далее считать, что векторы $\mathbf{p}$ и $\mathbf{q}$ в обозначениях векторов состояния $|\mathbf{p}\rangle_1$ и $|\mathbf{q}\rangle_2$ это двумерные векторы - это составляющие трёхмерных векторов импульса фотонов 1 и 2, поперечные к усреднённым направлениям пучков 1 и 2.

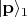
Будем также считать, что все векторы состояний в наших формулах относятся в пространстве к плоскостям (поперечным к усреднённым направлениям пучков) перед линзой и перед щелями. Т.е. $|\mathbf{p}\rangle_1$ это состояние фотона 1 перед линзой, $\mathbf{p}$ - двумерная часть импульса фотона 1, поперечная к направлению от кристалла на линзу, описывающая случайное отклонение вектора импульса фотона 1 от этого направления. 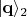И при этом $|\mathbf{q}\rangle_2$ - состояние фотона 2 перед заслонкой с щелями; $\mathbf{q}$ - двумерная часть импульса фотона 2, поперечная к направлению от кристалла на препятствие с щелями, описывающая флуктуацию вектора импульса фотона 2.

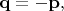
Тогда в каждой паре фотонов $\mathbf{q}=-\mathbf{p},$ так как суммарный вектор импульса в каждой паре один и тот же, не является флуктуирующей величиной. Такая корреляция описывается амплитудами вероятности с символом Кронекера:

$$C_{\mathbf{p},\mathbf{q}}=C_{\mathbf{p}}\,\delta_{-\mathbf{p},\mathbf{q}}$$

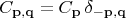
и вектор состояния пары есть

$$|\Psi\rangle=\sum_{\mathbf{p}}C_{\mathbf{p}}\,|\mathbf{p}\rangle_1\otimes|-\mathbf{p}\rangle_2$$

Условие нормировки:

$$\sum_{\mathbf{p}}|C_{\mathbf{p}}|^2=1$$

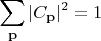
На практике распределение вероятности $|C_{\mathbf{p}}|^2$ для поперечного импульса, наверное, может в каком-то приближении описываться как гауссовское, с некоторым средним значением для $|\mathbf{p}|$ и с некоторой шириной. И, возможно, из-за специфики преобразования конкретным кристаллом фотонов от лазера в коррелированные пары ширина у пучков будет разная в разных поперечных направлениях; например, найдётся выделенное направление, около которого в основном и флуктуирует $\mathbf{p}.$ Причём, двумерная переменная $\mathbf{p}$ является непрерывной, сумма по ней понимается как двукратный интеграл (а символ Кронекера как дельта-функция).

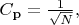
Но в этом месте я перехожу к сильно упрощённому описанию: для простоты будем считать все значения $\mathbf{p}$ равновероятными, притом дискретными и принимающими пусть очень большое, но конечное число $N$ значений. Тогда можем положить $C_{\mathbf{p}}=\frac{1}{\sqrt{N}},$ так что

$$|\Psi\rangle=\sum_{\mathbf{p}}\frac{1}{\sqrt{N}}\,|\mathbf{p}\rangle_1\otimes|\mathbf{-p}\rangle_2\qquad (a)$$

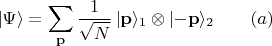
Теперь у нас всё готово, чтобы начать разбираться с главным вопросом: что и как регистрируется детекторами, какие "записи в лабораторном журнале" накапливаются, как и зачем ведётся счёт совпадений.

а) Вспомним, как тонкая линза создаёт изображение (перевёрнутое) далёких предметов на экране в фокальной плоскости, "focal plane".

Параллельные лучи света, широким пучком падающие на линзу с большой площадью (это как бы фотоны с точно определённым вектором импульса и с неопределёнными координатами внутри пучка, приходящие из источника в плоскость перед линзой), "фокусируются в одну точку" на экране за линзой. Если далёкий источник света находится на прямой, перпендикулярной плоскости линзы, "точка" будет в центре экрана. Если же свет приходит со стороны, т.е. по направлению, не строго перпендикулярному плоскости линзы, то точка на экране будет смещённой в противоположную сторону на соответствующее расстояние - тем большее, чем больше отклонение $\mathbf{p}$ импульса фотонов от перпендикуляра к линзе.

В принципе, так же измеряется импульс $\mathbf{p}$ фотона 1 при малой интенсивности света в пучке 1, т.е. в режиме счёта отдельных фотонов. Аппаратура "записывает в журнал" время появления сигнала от "точки", т.е. от фоточувствительного пикселя на детектирующем экране D1, расположенном в фокальной плоскости линзы, и записывает номер (или координаты) этого пикселя. Тем самым записываются данные, которыми при известной геометрии опыта определяются значения $\mathbf{p}$ каждого фотона 1. 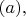От фотона к фотону вектор $\mathbf{p}$ случайным образом изменяется, флуктуирует; согласно модельному выражению $(a),$ вероятность каждого возможного значения $\mathbf{p}$ есть $1/N.$

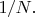
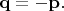
При этом у фотонов 2 должно быть $\mathbf{q}=-\mathbf{p}.$ Т.е. это тоже флуктуирующая величина, поэтому на детектирующем экране D2 за щелями в целом в итоге не образуется "интерференционной картины". Математического описания состояния фотонов 2 за щелями, как и фотонов 1 за линзой, я не привожу; мы будем лишь следить за возможностью выявления "интерференционной картины" в накопленных отсчётах на экране D2.

Аппаратура также "записывает в журнал" время появления сигнала от фоточувствительного пикселя на детектирующем экране D2, расположенном за препятствием с щелями, и записывает номер (или координаты) этого пикселя.

Затем мы, ну или сама аппаратура, сортируем записи, осуществляем "счёт совпадений". Прежде всего объединяем в одну строчку данные от D1 и D2, относящиеся к фотонам из одной и той же пары; непарные записи (а они есть, так как не все фотоны 2 проникают к экрану D2 сквозь препятствие с щелями) вычёркиваем вон. 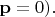Затем группируем строчки так, чтобы в одну группу попали данные от D1 с одним и тем же $\mathbf{p}$ (например, с $\mathbf{p}=0).$ Вот в такой группе, т.е. в отсортированных именно так данных D1 и D2 обнаруживается интерференционная картина.

Дело в том, что, говоря на языке аналогии с волнами, для формирования отчётливой интерференционной картины нужно, чтобы волны, приходящие в заданную точку экрана D2, имели стабильную во времени разность фаз. Для этого нужно, чтобы и у падающей на узкие щели волны разность фаз в местах расположения щелей была стабильной. Она определяется расстоянием между щелями, длиной волны $\lambda$ и направлением волнового вектора падающей плоской волны по отношению к плоскости со щелями. 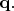Т.е., на нашем фотонном языке, нужна стабильность $\mathbf{q}.$ Поскольку "запутанность" здесь проявляется в том, что вектор $\mathbf{q}$ однозначно связан с вектором $\mathbf{p},$ который измеряется детектором D1, то, как видим, для выявления интерференции нужна указанная сортировка записей по признаку $\mathbf{p}=\operatorname{const}.$


б) Опыт с отодвинутым в "image plane" детектирующим экраном D1.

Исходя из текста статьи Zeilinger, можно предположить, что в этой постановке опыта измеряется двумерный радиус-вектор $\mathbf{x}$ фотона 1 перед линзой в плоскости, перпендикулярной, направлению на кристалл-источник. Поперечный импульс $\mathbf{p}$ в таких измерениях не имеет определённого значения. Тогда простейшее модельное описание перехода к этой постановке опыта сводится к двумерному "преобразованию Фурье" (дискретному, в данном упрощённом изложении). Записываем разложение векторов состояний с определёнными $\mathbf{p}$ для фотонов 1 по новому ортонормированному базису - по состояниям с определёнными $\mathbf{x}:$

$$|\mathbf{p}\rangle_1=\sum_{\mathbf{x}}|\mathbf{x}\rangle_1\,\langle \mathbf{x}|\mathbf{p}\rangle$$

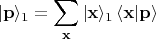
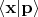
где числовые коэффициенты $\langle \mathbf{x}|\mathbf{p}\rangle$ это известные из курса квантовой механики выражения для комплексных значений волновой функции в форме плоской волны:

$$\langle \mathbf{x}|\mathbf{p}\rangle=\frac{1}{\sqrt{N}}\,e^{i\mathbf{p}\cdot\mathbf{x}/\hbar}$$

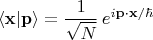
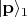
И подставляем разложенные так $|\mathbf{p}\rangle_1$ в $(a):$

$$|\Psi\rangle = \sum_{\mathbf{x}}\sum_{\mathbf{p}}\frac{1}{\sqrt{N}}\,\langle \mathbf{x}|\mathbf{p}\rangle\,|\mathbf{x}\rangle_1\otimes |-\mathbf{p}\rangle_2$$

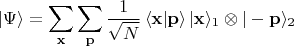
Заметим, что

$$\langle \mathbf{x}|\mathbf{p}\rangle = (\langle \mathbf{x}|-\mathbf{p}\rangle )^* = \langle \mathbf{-p}|\mathbf{x}\rangle$$

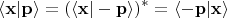
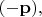
и поскольку суммирование по всем $\mathbf{p}$ это то же самое, что суммирование по всем $(-\mathbf{p}),$ то

$$\sum_{\mathbf{p}}|-\mathbf{p}\rangle_2\,\langle \mathbf{-p}|\mathbf{x}\rangle = |\mathbf{x}\rangle_2$$

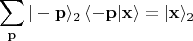
Таким образом, то же самое запутанное состояние $|\Psi\rangle$ по отношению к новому способу детектирования фотонов 1 можно представить в виде

$$|\Psi\rangle=\sum_{\mathbf{x}}\frac{1}{\sqrt{N}}\,|\mathbf{x}\rangle_1 \otimes |\mathbf{x}\rangle_2 \qquad (b)$$

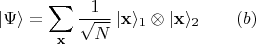
Видно, что в этой постановке опыта нахождение фотона 1 в "точке" $\mathbf{x}$ где-то в плоскости перед линзой скоррелировано с нахождением фотона 2 в соответствующей "точке" $\mathbf{x}$ где-то в плоскости перед препятствием с щелями.

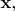
Аппаратура "записывает в журнал" время появления сигнала от фоточувствительного пикселя на детектирующем экране D1, расположенном в "image plane", и записывает номер (или координаты) этого пикселя. Тем самым записываются данные, которыми при известной геометрии опыта определяются значения радиальных координат $\mathbf{x},$ которые были у фотона 1 где-то в плоскости перед линзой. 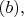От фотона к фотону этот вектор $\mathbf{x}$ флуктуирует; согласно модельному выражению $(b),$ вероятность каждого возможного значения $\mathbf{x}$ есть $1/N.$

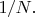
И по-прежнему аппаратура "записывает в журнал" время появления сигналов от фоточувствительных пикселей на детектирующем экране D2 за препятствием с щелями, и записывает номера (или координаты) этих пикселей.

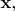
Сортировать эти данные "по импульсу" теперь невозможно, так как импульс в этой постановке опыта не измеряется. Можно сортировать данные по значениям $\mathbf{x},$ которые в принципе определяются из данных детектора D1. Например, можно выделить в одну группу те данные детектора D1, которым при счёте совпадений должно в пучке 2 соответствовать положение $\mathbf{x}$ фотонов 2 напротив одной из щелей. Распределение отсортированных так отсчётов D2 будет иметь вид какого-то пика - с максимумом напротив этой щели. Аналогично можно выделить группу данных о прохождении фотонов 2 в основном через другую щель. Понятно, что объединённая картина отсчётов D2 из этих групп данных будет похожа на классическую картину прохождения частиц через две щели без интерференции - получатся два максимума, по одному напротив каждой из щелей.

Что-то более конкретное сказать по такой упрощённой модели о реальных экспериментах Цайлингера и Допфер затрудняюсь. Ну, в принципе, главное понятно: как и почему вариант опыта (а) подходит для выявления "двухщелевой интерференцию в эксперименте с запутанными фотонами", а вариант (б) нет.

[chislo_avogadro]

chislo_avogadro в сообщении #1710380 писал(а):

Там неясно, проводился ли этот эксперимент в рамках диссертации или ...

Судя по описанию, всё же этот эксперимент был там проведен, причём с отложенным выбором. Выбор организован, как мне показалось, довольно остроумно.



Рисунок 4.39.: Схема нашего эксперимента с отложенным принятием решения: схема полностью аналогична схеме для микроскопа Гейзенберга. Однако конструкция за линзой модифицирована с помощью светоделителя, следующего за линзой Гейзенберга, и дополнительного детектора

Dopfer писал(а):

Расстояние между кристаллом LiIO3 и фотодиодом детекторного блока D2 составляет 34 см. Расстояние намного меньше, чем 105 см от кристалла до нашей точки принятия решения (светоделителя). Холостой фотон прошел двойную щель и был обнаружен еще до того, как сигнальный фотон попал на светоделитель, и способ измерения определяется случайным образом путем пропускания или отражения фотона.

Принимая во внимание данные микроскопа Гейзенберга, которые демонстрируют интерференционную картину при измерении импульса и дифракционную картину без какой-либо интерференции при измерении положения, можно задаться вопросом, как холостой фотон (со стороны двойной щели) может узнать, разрешено ли ему приземлиться в позиции интерференционного минимума или нет, если решение о типе измерения еще не принято.

Парадокс разрешается, если рассматривать измерительный прибор и измеряемый объект как единое целое. Двухфотонное состояние - это неразрывное целое и нечто большее, чем ”две частицы”. Только при обнаружении совпадений измеряется двухфотонное состояние, и только здесь можно наблюдать зависимость интерференционного контраста от типа измерения.
...
Подводя итог, мы не смогли обнаружить ни малейшей экспериментально наблюдаемой разницы между данными, где метод измерения был определён с задержкой, и данными, где метод измерения был определён заранее. Измерения подтверждают копенгагенскую интерпретацию квантовой механики.

realeugene в сообщении #1710388 писал(а):

Отложенным выбором называют селекцию статистики результатов пар измерений по какому-то критерию?

Ну вот выше как раз это описано. "Отложенный" он там потому, что 2-й фотон уже зарегистрирован, а первый ещё даже не долетел до делителя. Если мыслить фотоны в таком полуклассическом виде. А на делителе и происходит выбор типа измерения. Выбор случаен.

realeugene в сообщении #1710388 писал(а):

Классическая электронная схема совпадения очевидно для этого не нужна.

Во всех такого рода экспериментах, как я вижу, устанавливаются схемы совпадения. Видимо это, по крайней мере, облегчает постселекцию результатов.

[realeugene]

chislo_avogadro в сообщении #1710427 писал(а):

"Отложенный" он там потому, что 2-й фотон уже зарегистрирован, а первый ещё даже не долетел до делителя. Если мыслить фотоны в таком полуклассическом виде. А на делителе и происходит выбор типа измерения. Выбор случаен.

Выбор способа измерения фотона-1. Результаты измерения фотона-2 никак от этого выбора не зависят. А фотон-1 измеряется после этого выбора. И в зависимости от этого выбора показывает интерференцию в совместном распределении с фотоном-2 или нет. Почему же выбор "отложенный"? После чего?

-- 24.11.2025, 00:17 --

chislo_avogadro в сообщении #1710427 писал(а):

Видимо это, по крайней мере, облегчает постселекцию результатов.

Просто меньше поток данных, если игнорировать одиночные события.

[chislo_avogadro]

realeugene в сообщении #1710432 писал(а):

Выбор способа измерения фотона-1. Результаты измерения фотона-2 никак от этого выбора не зависят. А фотон-1 измеряется после этого выбора. И в зависимости от этого выбора показывает интерференцию в совместном распределении с фотоном-2 или нет. Почему же выбор "отложенный"? После чего?

Вы, как вижу, даёте собственное определение "отложенности" выбора, отличное от общепринятого.
И не хотите видеть в этом эксперименте парадокса.

В эксперименте, указанном ТС, тоже, казалось бы, был парадокс, но Cos(x-pi/2) посмотрел оригинал статьи и указал, что фотоны определённой поляризации задерживаются поляризатором, отсчёты на щелях лишаются подтверждения на счётчике совпадений и должны быть отброшены. Тем самым парадокс там исчезает.

Но вот в эксперименте Допфер с отложенным выбором потерь фотонов нет. Может быть Cos(x-pi/2) найдёт время развенчать и это понимание, но пока что потерь фотонов не видно.
И тогда возникает парадокс, Допфер в приведённом тексте про это пишет (с указанием, как этот парадокс разрешается).

Пусть фотон 2 регистрируется в точке, где, при наличии интерференции, нулевая вероятность (тут идеализирую) попадания фотона. А 1-й фотон, уже после регистрации 2-го, выбрал путь к линзе, которая не позволяет определить импульс, т.е. информация wich way стирается. Получается, 1-й фотон оказался там, где ему быть нельзя.

Всё это, конечно, в представлении о фотонах как о движущихся частицах.

[realeugene]

chislo_avogadro в сообщении #1710456 писал(а):

Вы, как вижу, даёте собственное определение "отложенности" выбора, отличное от общепринятого.

Я пытаюсь у вас выяснить, чем "общепринятое" определение в вашем понимании отличается от изложенного мною? Мне сейчас представляется, что "отложенный выбор" как название не более, чем хайп.

-- 24.11.2025, 14:35 --

chislo_avogadro в сообщении #1710456 писал(а):

Пусть фотон 2 регистрируется в точке, где, при наличии интерференции, нулевая вероятность (тут идеализирую) попадания фотона.

Так нет такой точки. Интерференция наблюдается только при наложении каких-то условий на состояние фотона-1 в совместной статистике их наблюдений. От выбора способа измерения фотона-1 маргинальное распределение измеренного положения фотона-2 не зависит никак, если фотон-1 сам размазан по пространству состояний широко. Осреднение по неизмеряемому состоянию фотона-1 только сглаживает интерференционные полосы вплоть до их исчезновения, если фотон-1 размазан достаточно широко.

UPD: Точнее, статистика одиночных измерений фотона-2 никак не зависит от выбора способа измерения фотона-1 в любом случае, и даже от того, производится ли над ним какое-то измерение или оптическая ось там перекрыта чёрной перегородкой. Иначе можно было бы организовать канал передачи информации в прошлое. Так что все чудеса наблюдаются только в условных распределениях по совпадению с фотоном-1, измеренном в каком-то состоянии.

[Cos(x-pi/2)]

chislo_avogadro в сообщении #1710456 писал(а):

Пусть фотон 2 регистрируется в точке, где, при наличии интерференции, нулевая вероятность (тут идеализирую) попадания фотона. А 1-й фотон, уже после регистрации 2-го, выбрал путь к линзе, которая не позволяет определить импульс, т.е. информация wich way стирается. Получается, 1-й фотон оказался там, где ему быть нельзя.

Во втором предложении что-то перепутано.

chislo_avogadro

И суть дела не в потерях фотонов, а в том, что конкретно представляют собой данные опыта и по какому рецепту они группируются (сортируются) при счёте совпадений. Выше в "простыне" я подробно описал всё это в упрощённой модели векторов состояния, соответствующей эксперименту Допфер; (упрощение там у меня не принципиальное, а связано только с тем, что я не стал учитывать не очень-то простую реальную картину пучков света, возникающих при параметрическом преобразовании лазерного луча накачки нелинейным кристаллом, а для упрощения математики заменил её равномерным распределением поперечных составляющих импульса в пучках.) Ниже пользуюсь понятиями и обозначениями из той "простыни".

Так вот: до того, как будет зарегистрирован фотон 1, невозможно утверждать, будто << фотон 2 регистрируется в точке, где, при наличии интерференции, нулевая вероятность >>. Потому что картина интерференции (т.е. в каких точках детектирующего экрана D2, установленного за препятствием с щелями, получатся минимумы и максимумы при счёте совпадений), зависит от импульса $\mathbf{q}$ фотонов 2 на подлёте к щелям.

Поясняю подробно. Допустим, в какой-то фиксированной точке экрана D2 находится минимум некоторой интерференционной картины, - такой картины, которая получается, когда все подлетающие к щелям фотоны имеют специальное конкретное значение своего импульса: $\mathbf{q}=\mathbf{q}'.$ Вопрос: а имеют ли вообще все подлетающие к щелям фотоны 2 именно импульс $\mathbf{q}'\,?$

Ответ: нет. Фотоны 2, подлетающие к щелям, могут иметь разные импульсы, их импульс $\mathbf{q}$ это квантово-механически флуктуирующая (от фотона к фотону) величина, определяемая при измерениях импульса.

Нужный (для образования данной интерференционной картины) импульс $\mathbf{q}'$ имеют вследствие коррелированности пар только те фотоны в пучке 2, у которых их партнёры по паре в пучке 1 имеют специальное конкретное значение импульса $\mathbf{p}=\mathbf{p}'.$ (В модели в "простыне" выше речь идёт о поперечных составляющих импульса, и обсуждаемое сейчас условие для этих поперечных импульсов выглядит так: $\mathbf{q}'=-\mathbf{p}'.$ Но важна не именно эта конкретика, а сам факт строгой коррелированности значений импульса, в этом заключается квантовая "запутанность по импульсу" в парах фотонов: импульсам $\mathbf{q}$ взаимно однозначно соответствуют импульсы $\mathbf{p}.)$

Если фотоны в пучке 1 будут иметь другое конкретное значение импульса, $\mathbf{p}=\mathbf{p}'',$ то их партнёры в пучке 2 будут иметь тоже другой импульс: $\mathbf{q}=\mathbf{q}''.$ Такие фотоны 2, т.е. имеющие на подлёте к щелям фиксированный импульс $\mathbf{q}'',$ тоже дадут на экране D2 интерференционную картину, но она будет другая - сдвинутая по сравнению с картиной от фотонов 2 с импульсом $\mathbf{q}'.$ Максимумы этой второй картины могут оказаться на месте минимумов первой картины, или где-то между.

И так далее: у фотонов в пучке 1 с импульсом $\mathbf{p}'''$ партнёры в пучке 2 имеют определённый импульс $\mathbf{q}''',$ и после накопления множества отсчётов образуют на экране D2 какую-то свою, третью, интерференционную картину.

Какую из всех возможных интерференционных картин мы получим в результате счёта совпадений - это зависит от того, в какой точке детектирующего экрана D1, установленного на расстоянии $f$ за линзой, мы будем регистрировать события для счёта совпадений. При установке детектора D1 на расстоянии $f$ за линзой разным пикселям на фоточувствительной детектирующей панели D1 соответствуют разные значения импульса $\mathbf{p}$ фотонов 1 (речь об импульсе фотона 1 на подлёте к линзе): $\mathbf{p}'\,,$ $\mathbf{p}''\,,$ $\mathbf{p}'''$ и т.д.

Если детектор D1 находится на расстоянии $2f$ за линзой, то сигналам от разных его пикселей соответствуют уже не разные значения импульса $\mathbf{p}$ фотонов 1, а разные значения радиальной координаты фотона 1. Это - информация о положении фотона 1 в поперечном сечении пучка. Импульс и координата не могут одновременно иметь определённые значения. Математика квантовой механики показывает, что в этом случае, набрав в конкретной фиксированной точке экрана D1 зарегистрованные события для счёта совпадений с событиями в детекторе D2, мы получаем информацию о положении фотонов-партнёров перед щелями: это "информация which way" о фотонах 2.

Набор событий в D2, зарегистрированных в таких совпадениях с событими в D1 (т.е. когда детектор D1 установлен на расстоянии $2f$ за линзой), мы не можем сортировать на группы с определёнными импульсами $\mathbf{q}'\,,$ $\mathbf{q}''\,,$ $\mathbf{q}'''$ и получать в каждой группе свою интерференционную картину, как было в том варианте опыта. Потому что в этом варианте опыта импульсы фотонов не являются определёнными и не измеряются. Значит, ни про какое событие в этом наборе не следует говорить, что "фотон 2 попал в минимум интерференционной картины": в этом варианте опыта нет интерференционных картин.

"Парадоксальным" могло бы выглядеть вот какое рассуждение. << Пусть фотон 2 регистрируется в точке, где нулевая вероятность при наличии интерференции фотонов 2 с конкретным импульсом $\mathbf{q}'.$ Затем зеркало переключили так, что партнёр-фотон 1 пошёл к детектору D1, находящемуся на расстоянии $f$ за линзой, и попал там в пиксель, соответствующий импульсу $\mathbf{p}'.$ Импульсу $\mathbf{p}'$ соответствует интерференционная картина фотонов 2 с импульсом $\mathbf{q}'$ - у неё минимум как раз там, куда почему-то уже попал фотон 2. Получается, один из этих двух фотонов ошибся? Т.е. либо фотон 2 попал туда, куда ему нельзя попадать, либо фотон 1 попал не туда, куда надо: он должен был бы обнаружиться не с импульсом $\mathbf{p}',$ а с каким-то другим, например с $\mathbf{p}''$ (тогда у фотона 2 был бы импульс $\mathbf{q}''\neq \mathbf{q}',$ и ему не запрещалось бы попадать в минимумы чужой интерференционной картины, т.е. соответствующей импульсу $\mathbf{q}').$ >> *)

Тут понятно, что ошибка заключается в рассуждении - в произвольности предположений типа "пусть фотон 2 попал туда, а фотон 1 попал сюда". Мы не имеем права решать, куда попадать фотонам. Квантовая корреляция на то она и корреляция, что именно она решает, что должно случиться. Фотоны не ошибутся. Если фотон 2 попал в минимум интерференционной картины, соответствующей импульсу $\mathbf{q}',$ и затем мы измеряем импульс партнёра-фотона 1, то этот импульс обязательно окажется тем самым нужным импульсом $\mathbf{p}''\neq \mathbf{p}' ,$ который диктуется корреляцией импульсов в паре фотонов, свойственной рассматриваемому запутанному состоянию. "Парадокса" нет, просто есть квантовая специфика квантовых состояний.

Альтернативное возможное рассужденьице (в попытке придумать "парадокс"): << Пусть фотон 2 регистрируется в точке, где нулевая вероятность при наличии интерференции фотонов 2 с конкретным импульсом $\mathbf{q}'.$ Затем зеркало переключили так, что партнёр-фотон 1 пошёл к детектору D1, находящемуся на расстоянии $2f$ за линзой, и попал там в пиксель, соответствующий координате фотона $\mathbf{x}'.$ >>

Тут вообще не вышло никакого парадокса. При регистрации фотона 1 таким детектором D1 совпадения с событиями в D2 не образуют интерференционной картины. Поэтому нельзя сказать, что фотон 2, попав в минимум некоей интерференционной картины, "попал туда, куда ему нельзя попадать". В этом наборе совпадений событий D1 и D2 фотону разрешено попадать туда, куда ему нельзя было бы попадать в другом наборе совпадений (т.е. наблюдаемых при другом расстоянии между линзой и детектором D1).

P.S *) отредактировал этот пост; извините, сначала что-то не то написал.