О критериях качества генераторов псевдослучайных чисел

[Dig386]

warlock66613 писал(а):

На кой чёрт, извините, мне в этих задачах криптостойкость (во втором случае она откровенно даже вредна, ибо надо максимально быстро генерить, а качество совершенно неважно)?

Вам там была действительно нужна скорость быстрее 1 ГиБ/с? Если да, то даже с rand() могут быть серьезные проблемы из-за мьютексов. Если не нужна, то проблем с хорошо реализованным шифром у Вас бы не было. В случае выборка цвета графика шифр тем более подходит, т.к. затраты на его работу будут пренебрежимо малы.

Цитата:

качество совершенно неважно

Если совершенно неважно, то подошел ли бы мой пример с DEADBEEF-счетчиком? Если "совершенно неважно" - то наверняка бы подошел?

Цитата:

И почему вы считаете что ваши задачи важнее моих?

Не считаю. Я просто защищаю универсальные решения с разумным быстродействием, которые подошли бы в подавляющем большинстве ситуаций.

[mihaild]

Dig386 в сообщении #1709808 писал(а):

Модуль, укладывающийся в 32 бита - это период, исчерпывающийся за минуты, а то и вообще за несколько секунд.

Речь же была про учебники. Причем не специализированные (в специализированных итак уже про LCG не пишут, потому что про него уже должны знать).

Dig386 в сообщении #1709808 писал(а):

Если ничего не менять вообще - то на man страницу нужно добавить четкое предупреждение о непригодности алгоритма для научных и инженерных расчётов. И вообще сказать, что он тут только для совместимости оставлен, а статистическое качество ужасно.

Это универсальное предупреждение. "Прежде чем использовать инструмент для чего-то важного, выясните, что он делает, и убедитесь, что он делает то, что вам нужно".

Dig386 в сообщении #1709808 писал(а):

Каких именно приложений?

Я пример уже писал - случайная задержка при перезапросах.

Dig386 в сообщении #1709808 писал(а):

если Вы не можете использовать ГПСЧ вида $x_n = (x_{n-1} + \mathrm{DEADBEEF}_{16}) \mod 2^{32}$, то rand() из стандартной библиотеки языка Си Вам не подойдет

Вот конкретно для перезапросов стандартный подходит, в Ваш - нет. Потому что если значения при двух независимых вызовах получились близкими, то и следующие за ними будут близкими.

Dig386 в сообщении #1709808 писал(а):

В glibc я ChaCha не засовывал, но получается у меня так на Intel(R) Core(TM) i5-11400H

А на 3м пентиууме? Или хотя бы на атоме 10летней давности?

Dig386 в сообщении #1709821 писал(а):

Вам там была действительно нужна скорость быстрее 1 ГиБ/с?

Возможно там нужно было делать что-то кроме генерации случайных чисел.

[Dig386]

mihaild писал(а):

Речь же была про учебники. Причем не специализированные

Тем более не нужно пихать туда всякую ерунду и забивать голову, сразу должен быть ARX-шифр как универсальный рабочий инструмент и "тест на следующий бит" как критерий качества ГПСЧ общего назначения (даже не для крипто). А то они взглянут на 32-битный или 64-битный LCG и всерьёз подумают, что так можно делать, хотя на самом деле обычно нельзя. Хакеры же доберутся до сверхскоростных ГПСЧ сами.

mihaild писал(а):

А на 3м пентиууме? Или хотя бы на атоме 10летней давности?

Вот бенчмарки на древнем железе:
https://cr.yp.to/chacha.html
Да, результаты там похуже. Но и не прям "ужас-ужас". Сейчас с аналогичной скоростью функции rand() из glibc все как-то мирятся и даже не думают об этом.

Цитата:

Потому что если значения при двух независимых вызовах получились близкими,

Вы точно проверяли статистическими тестами Ваше предположение о "не получились близкими"? И точно уверены, что там не нужно использовать вообще /dev/urandom для исключения какого-то вредительства со стороны из-за предсказуемости задержек? Или если задержки пойдут с разных компьютеров - что паттерны LCG от разных сидов не устроят отказ в обслуживании? Проводили такую симуляцию методом Монте-Карло?

Цитата:

Это универсальное предупреждение. "Прежде чем использовать инструмент для чего-то важного, выясните, что он делает, и убедитесь, что он делает то, что вам нужно".

Бесспорно. Но я всё еще не понимаю, почему с банальным квадратным корнем подход разработчиков стандартной библиотеки языка Си несравненно более ответственный (нормальная реализация), чем в случае функции rand() (наколенная поделка из музея).

[mihaild]

Dig386 в сообщении #1709834 писал(а):

Тем более не нужно пихать туда всякую ерунду и забивать голову, сразу должен быть ARX-шифр как универсальный рабочий инструмент

А первоклассникам вместо подсчета клеточек нужно сразу рассказывать интегральное исчисление. Чтобы блочные шифры не выглядели магией "вот тут так переложите биты, и не спрашивайте, почему", нужно потратить больше времени, чем обычно есть в курсе.

Dig386 в сообщении #1709834 писал(а):

А то они взглянут на 32-битный или 64-битный LCG и всерьёз подумают, что так можно делать, хотя на самом деле обычно нельзя.

На самом деле обычно можно. А там, где нельзя - в криптографии или продвинутых ЧМах - про это должны рассказывать отдельно.

Dig386 в сообщении #1709834 писал(а):

Вот бенчмарки на древнем железе

Там нет сравнения с другими вариантами.

Dig386 в сообщении #1709834 писал(а):

Вы точно проверяли статистическими тестами Ваше предположение о "не получились близкими"?

Я могу оценить поведение линейной рекурренты в уме без статистических тестов :) Разность между двумя сериями умножается на каждом шаге на тот же множитель.

Dig386 в сообщении #1709834 писал(а):

Но я всё еще не понимаю, почему с банальным квадратным корнем подход разработчиков стандартной библиотеки языка Си несравненно более ответственный (нормальная реализация), чем в случае функции rand() (наколенная поделка из музея)

Потому что имеющийся rand тоже очень много где пригоден. Собственно я бы сказал, что если кому-то он не подходит - то этот кто-то должен достаточно хорошо понимать, что делает.
Можно ли было бы аналогично сделать какой-то шустрый неточный sqrt? Да наверное можно было бы.
Важно то, что 1) это в любом случае компромиссы; 2) выбор сделан 50 лет назад, и поменять его уже нереально.

[Евгений Машеров]

Дело в том, что требования к генератору противоречивы. Случайность не есть закономерность, а мы требуем случайное с надлежащим законом. При этом "действительно случайные" могут выглядеть совершенно не случайно. Если мы встретим в выдаче ГСЧ ряд из тысячи нулей без единой единицы, то заподозрим. что это плохой ГСЧ. Но в последовательности независимо появляющихся случайных нулей и единиц должен появиться такой ряд, иначе это уже не будут независимые величины, получив 999 нулей, мы тогда сможем точно угадать следующее - единицу.
Поэтому все ГСЧ плохи, но некоторые применимы в своей области. Если нам нужен ГСЧ для криптографии - важнее всего непредсказуемость, если для Монте-Карло - равномерность. Разумеется, где-то застряли древние ГСЧ, скверные с точки зрения любых критериев, и никто этого не замечает, поскольку требования к ним ограничены, а менять на новый - труд, и немалый.
Чего-то мне вспомнилось, что подобные темы регулярно всплывают, вот, скажем, почти десятилетней давности
topic110640.html
(там ещё, под "оффтопиком", моя байка из студенческих времён, о "супер-ГСЧ")

[Dig386]

mihaild писал(а):

Чтобы блочные шифры не выглядели магией "вот тут так переложите биты, и не спрашивайте, почему", нужно потратить больше времени, чем обычно есть в курсе.

Магия будет и при LCG в духе "вот константы, кривыми руками не трогать, а то плохо будет". А чтобы их подобрать - нужно изучать хотя бы второй том Кнута, уметь запускать спектральный тест, BigCrush и PractRand. Ну и в шифре тоже константы. А вообще что качественный ГПСЧ в виде шифра может оказаться "черным ящиком" - это нормально, всё в жизни освоить нельзя. Впрочем, простейшие опыты в духе "сделай свой некриптографический ГПСЧ на основе сети Фейстеля, измеряя лавинный эффект и гоняя PractRand" - это вообще уровень продвинутой лабораторки, т.е. сам принцип показать можно. И для многопоточных случаев это будет даже проще LCG. А если не углубляться в теорию, то ChaCha с напутствием "вот константы, вот алгоритм, вот тестовые вектора, кривыми руками не лезть" - вполне нормально.

Цитата:

На самом деле обычно можно.

"Обычно" - это где? У меня получается, что 32-битный LCG - почти нигде нельзя, особенно если там m=2^32:
1) Интегрирование по Монте-Карло? Да ни в коем случае.
2) Рассчитать какой-то квантиль распределения тем же методом Монте-Карло, например, для Dixon's Q-test? Да у него период раньше закончится, чем мы получим хотя бы "до 4 знака после запятой".
3) Оценить погрешность косвенного измерения без дифференцирования? Тоже нельзя.
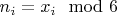
4) Выбрать грань игрального кубика в игре по формуле $n_i = x_i \mod 6$? Опять ерунда получается.
5) Выбрать пивот для QuickSort? Тут очень желателен вообще системный API для генерации криптографических ключей.
6) Сгенерировать "белый шум" на экране? Так кто ж знает, что получится-то, опять засада.
7) Нарезать вывод на байты и получить равномерное распределение? Ничего не выйдет, т.к. такой ГПСЧ не подчиняется равномерному распределению.
8) Моделировать какой-то процесс из теории массового обслуживания? Лучше не надо.
Вот и получается, что ничего нельзя. Если уж показывать LCG, то нормальный, хотя бы вот такой, он хотя бы проходит BigCrush и PractRand и пригоден для использования в математической статистике (ссылку приводил ранее). И очень быстрый:

uint32_t MWC64X(uint64_t *state)
{
    uint32_t c=(*state)>>32, x=(*state)&0xFFFFFFFF;
    *state = x*((uint64_t)4294883355U) + c;
    return x^c;
}

Он приличный, т.к. там довольно большой простой делитель и "плохих младших бит" просто нет, а выход дополнительно скремблируется побитовым XOR. И уж эта шарманка точно проще генератора Wichmann-Hill-1982.

Цитата:

Там нет сравнения с другими вариантами.

Другие варианты на древнем железе были бы 0.5-1.5 cpb, ChaCha12 - около 7 cpb, устаревший и тормознутый 3DES - ближе к 100 cpb. Т.е. уже 20 лет назад шифры позволяли генерировать псевдослучайные числа со скоростью порядка сотен мегабайт в секунду, что обычно вполне достаточно. А недостаточно таких скоростей весьма специфическим людям, которые вполне могут написать свои ГПСЧ, скоростные.

Цитата:

Я могу оценить поведение линейной рекурренты в уме без статистических тестов :)

Не можете: одно выполнение спектрального теста Кнута займет в лучшем случае неделю "на бумажке". А базовая эмпирическая проверка качества линейной конгруэнции вручную невозможна, т.к. продолжительность человеческой жизни - обычно не более 4 гигасекунд, и человек не успеет провести нужный объем вычислений. Общепринятая же проверка качества некриптографического ГПСЧ вручную потребует десятки миллионов лет.

-- 19.11.2025, 19:57 --

Евгений Машеров писал(а):

Если мы встретим в выдаче ГСЧ ряд из тысячи нулей без единой единицы, то заподозрим. что это плохой ГСЧ. Но в последовательности независимо появляющихся случайных нулей и единиц должен появиться такой ряд, иначе это уже не будут независимые величины, получив 999 нулей, мы тогда сможем точно угадать следующее - единицу.

Не сможем угадать, вероятность того, что следующее - 1, все равно 0.5. Также все эти вопросы решаются через понятие колмогоровской сложности - минимальной длины программы, которой можно представить последовательность. И 1000 нулей подряд хорошо сжимаются. Впрочем, если последовательность длиннее 2^1000, то рано или поздно мы на подобные блоки нулей нарвемся. Но выиграть на сжатии не получится из-за накладных расходов на указание позиции в потоке и т.п.

Цитата:

Если нам нужен ГСЧ для криптографии - важнее всего непредсказуемость, если для Монте-Карло - равномерность.

Равномерность для метода Монте-Карло - это ослабленный вариант непредсказуемости, рожденный в эпоху слабости компьютеров и секретности криптографии. И качественный поточный шифр пригоден как ГПСЧ для метода Монте-Карло, иначе он не был бы шифром.

Цитата:

моя байка из студенческих времён, о "супер-ГСЧ")

Комбинированные генераторы - вещь достаточно известная, см. семейство KISS от Марсальи, но он делал для равномерного распределения.

Цитата:

а менять на новый - труд, и немалый.

Естественно, это - труд. И если уж его проделывать, то, возможно, надо менять сразу на поточные шифры.

[mihaild]

Чтобы цитировать, выделите цитируемый текст и нажмите кнопку "вставка" в правом нижнем углу цитируемого поста, нужный тег quote сгенерируется автоматически.

Dig386 в сообщении #1709906 писал(а):

Магия будет и при LCG в духе "вот константы, кривыми руками не трогать, а то плохо будет". А чтобы их подобрать - нужно изучать хотя бы второй том Кнута, уметь запускать спектральный тест, BigCrush и PractRand.

У Вас понятие "плохо" сильно выходи за рамки базовых курсов. Полный период - и хватит.

Dig386 в сообщении #1709906 писал(а):

Интегрирование по Монте-Карло?

Смотря что интегрируем.

Dig386 в сообщении #1709906 писал(а):

Выбрать грань игрального кубика в игре по формуле $n_i = x_i \mod 6$? Опять ерунда получается.

Почему?

Dig386 в сообщении #1709906 писал(а):

А недостаточно таких скоростей весьма специфическим людям, которые вполне могут написать свои ГПСЧ, скоростные

В качестве альтернативы могу предложить написать свои генераторы людям, которых не устраивает качество стандартных.

Dig386 в сообщении #1709906 писал(а):

Не можете: одно выполнение спектрального теста Кнута займет в лучшем случае неделю "на бумажке".

А мне не нужно прохождение спектрального теста для этой задачи.

Dig386 в сообщении #1709906 писал(а):

Также все эти вопросы решаются через понятие колмогоровской сложности

Колмогоровская сложность определена с точностью до аддитивной константы, говорить о сложности конкретной последовательности - моветон.

[Dig386]

mihaild в сообщении #1709917 писал(а):

У Вас понятие "плохо" сильно выходи за рамки базовых курсов. Полный период - и хватит.

И что же с ними делают в "базовых курсах"? И главное - чем приличный MWC64X сложнее ни на что не годного 32-битного LCG? И главное - даже в базовом курсе надо прививать культуру работы и предупреждать о негодных алгоритмах во многих ГПСЧ. В частности, о том, что на весь трехтомник TAOCP - то ли 2, то ли 3 хороших генератора, из которых все медленнее аппаратно ускоренных шифров. Но Кнуту простительно: пионерам-исследователям всегда тяжелее, чем их последователям, и Кнут честно предупреждал о том, что в будущем ГПСЧ из его книги могут быть признаны неудовлетворительными.

mihaild в сообщении #1709917 писал(а):

Смотря что интегрируем.

А зачем вообще разбираться во влиянии артефактов ГПСЧ на численное интегрирование, когда можно сразу взять хороший, да хоть Вихрь Мерсенна можно. Такое исследование "а можно ли плохой ГПСЧ тут использовать" - это уже очень продвинутый материал. Проще сказать "нет, нельзя".

mihaild в сообщении #1709917 писал(а):

Почему?

Потому что там в младшем бите может быть 0, 1, 0, 1, 0, 1, если делитель - степень двойки.

mihaild в сообщении #1709917 писал(а):

В качестве альтернативы могу предложить написать свои генераторы людям, которых не устраивает качество стандартных.

На данный момент стандарт де-факто в Excel, MATLAB, Python, Octave, R, и отчасти C++ - вихрь Мерсенна. Да, у него есть статистические дефекты, но их реально надо искать, и они почти нигде не мешают. И при его использовании хотя бы можно избежать исчерпания периода, решетчатых структур из точек в многомерном пространстве, малого периода отдельных бит, неравномерности распределения и т.п. В Rust вот ChaCha12 взяли, в golang протаскивают ChaCha8, в Julia и Lua - вроде бы xoroshiro++. А вот в Си и Java почему-то остаются треш-генераторы в стандартных библиотеках.

[Евгений Машеров]

Dig386 в сообщении #1709906 писал(а):

Не сможем угадать, вероятность того, что следующее - 1, все равно 0.5. Также все эти вопросы решаются через понятие колмогоровской сложности - минимальной длины программы, которой можно представить последовательность. И 1000 нулей подряд хорошо сжимаются. Впрочем, если последовательность длиннее 2^1000, то рано или поздно мы на подобные блоки нулей нарвемся. Но выиграть на сжатии не получится из-за накладных расходов на указание позиции в потоке и т.п.

О чём я говорю. Что последовательность из 1000 нулей будет казаться "неравномерной", и может возникнуть желание "доработать" генератор, чтобы выдавал поравномернее. В частности, чтобы последовательности из 1000 нулей не могло бы быть. Но тогда, получив 999 нулей, мы можем утверждать, что далее единица, "усовершенствованный генератор" тысячи нулей выдать не может. То есть противоречие между требованиями равномерности и непредсказуемости.

Dig386 в сообщении #1709906 писал(а):

Равномерность для метода Монте-Карло - это ослабленный вариант непредсказуемости, рожденный в эпоху слабости компьютеров и секретности криптографии. И качественный поточный шифр пригоден как ГПСЧ для метода Монте-Карло, иначе он не был бы шифром.

Это разные требования. Даже соглашаются вовсе отказаться от требования случайности, вместо этого используют "последовательности с низким расхождением"

[Dig386]

Евгений Машеров в сообщении #1709926 писал(а):

То есть противоречие между требованиями равномерности и непредсказуемости.

Вероятности порядка $2^{-1000}$ - на много порядков меньше вероятности сбоя аппаратуры, поэтому "1000 нулей" в реальной жизни и будут говорить о том, что мы видим какой-то артефакт генератора.

Цитата:

Это разные требования. Даже соглашаются вовсе отказаться от требования случайности, вместо этого используют "последовательности с низким расхождением"

Квазислучайные последовательности, например, последовательности Соболя - совсем другое дело, они успешно используются, но статистические тесты на случайность провалят. А вот ГПСЧ должен иногда давать сгущения и разрежения точек, иначе он не выглядел бы случайным. И насчёт разности требований: согласен, к шифру требования куда более жесткие. И если гамму потокового шифра можно и даже нужно использовать как ГПСЧ в методе Монте-Карло (если нельзя - то шифр непригоден для использования), но обратное неверно. Вообще этот ментальный разрыв между шифром и генератором псевдослучайных чисел для меня удивителен: потоковый шифр - это просто ГПСЧ очень высокого качества.

[warlock66613]

Dig386 в сообщении #1709934 писал(а):

Вероятности порядка $2^{-1000}$ - на много порядков меньше вероятности сбоя аппаратуры, поэтому "1000 нулей" в реальной жизни и будут говорить о том, что мы видим какой-то артефакт генератора.

Ага, а поскольку любая конкретная последовательность имеет точно такую же вероятность, то значит что бы ни выпало, нужно предполагать артефакт генератора.

[Dig386]

warlock66613 в сообщении #1709937 писал(а):

Ага, а поскольку любая конкретная последовательность имеет точно такую же вероятность, то значит что бы ни выпало, нужно предполагать артефакт генератора.

Если задать какую-то произвольную подпоследовательность достаточной длины и ждать ее выпадения - то вероятность встретить именно её очень мала. Но как только мы начинаем искать несколько таких последовательностей - нужны поправки на множественное сравнение. Другое дело, что "одни нули" нередко связаны с артефактами конкретных генераторов, например, плохо инициализированного вихря Мерсенна, поэтому их искать интереснее.

[Ende]

Тема перемещена из форума «Дискуссионные темы (М)» в форум «Программирование»
Причина переноса: ближе к фактическому предмету обсуждения.