Некоторые вопросы по интегральному исчислению

[Solaris86]

Здравствуйте!
В этой теме буду писать те вопросы, которые уже давно имеются, но найти на них ответы пока не удалось, а также те вопросы, которые будут возникать в дальнейшем.
Начну с вопроса про неопределённый интеграл
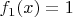
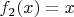
Начну издалека. Например, у меня есть 3 функции: $f_1(x)=1$, $f_2(x)=x$ и $f_3(x)=x^2$
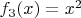
Сначала я ставлю себе такую задачу - найти множество всех касательных к каждой из этих функций.
Эту задачу помогает решить производная - $f'(x) = \lim\limits_{\Delta x \rightarrow 0} \frac{f(x+\Delta x)-f(x)}{\Delta x}$:
$f_1'(x) = \lim\limits_{\Delta x \rightarrow 0} \frac{f_1(x+\Delta x)-f_1(x)}{\Delta x} = \lim\limits_{\Delta x \rightarrow 0} \frac{1-1}{\Delta x} = \lim\limits_{\Delta x \rightarrow 0} \frac{0}{\Delta x} = 0$
$f_2'(x) = \lim\limits_{\Delta x \rightarrow 0} \frac{f_2(x+\Delta x)-f_2(x)}{\Delta x} = \lim\limits_{\Delta x \rightarrow 0} 1 = 1$
$f_3'(x) = \lim\limits_{\Delta x \rightarrow 0} \frac{f_3(x+\Delta x)-f_3(x)}{\Delta x} = \lim\limits_{\Delta x \rightarrow 0} (2x-\Delta x)= 2x$
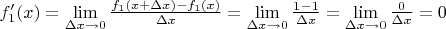
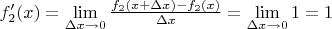
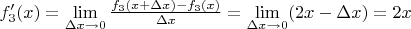
Мы получили формулы для расчёта расчёт тангенса угла наклона касательной в любой точке для каждого графика и, таким образом, множество всех касательных к каждой из этих функций.
Этот вопрос обычно очень подробно рассматривается во всех учебниках, даётся объяснение, как секущая устремляется к касательной, подробные картинки и т.п. Тут всё ясно.
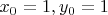
Найдём уравнения касательных для каждой функции в точке $x_0 = 1, y_0 = 1$ по формуле $y_\text{кас}(x_0)-y_0 = f'(x_0) \cdot (x-x_0)$:
$y_\text{кас}_1(x_0)-y_0 = f_1'(x_0) \cdot (x-x_0)$: $y_\text{кас}_1(1)-1 = 0 \cdot (x-1) \Rightarrow y_\text{кас}_1(1) = 1$
$y_\text{кас}_2(x_0)-y_0 = f_2'(x_0) \cdot (x-x_0)$: $y_\text{кас}_2(1)-1 = 1 \cdot (x-1) \Rightarrow y_\text{кас}_2(1) = x$
$y_\text{кас}_3(x_0)-y_0 = f_3'(x_0) \cdot (x-x_0)$: $y_\text{кас}_3(1)-1 = 2 \cdot 1 \cdot (x-1) \Rightarrow y_\text{кас}_3(1) = 2x-1$
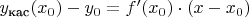
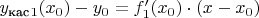
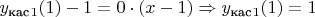
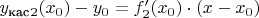
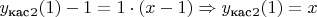
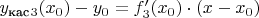
Далее, я ставлю себе обратную задачу - имея множество всех касательных к функции найти саму эту (первообразной) функцию (с точностью до константы). Вот тут появляется как раз понятие неопределённого интеграла и просто даётся уже готовая формула без вывода:
$f(x) + C = \int f'(x)dx$
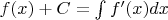
Вот я по формуле неопределённого интеграла получил для исходных функций такие выражения:
$f_1(x) + C_1 = \int f_1'(x)dx = \int 0 \cdot dx = 0$
$f_2(x) + C_2 = \int f_2'(x)dx = \int 1 \cdot dx = \int dx$
$f_3(x) + C_3 = \int f_3'(x)dx = \int 2x \cdot dx = \int 2xdx$
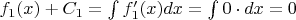
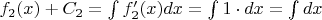
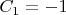
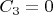
Теперь я хочу для (первообразной) функции узнать её значение (с точностью до константы, при этом зададим значение константы для каждой функции: $C_1 = -1$, $C_2 = 0$ и $C_3 = 0$) в точке $x_0 = 1$.
Тут возникает непонимание: неопределённый интеграл - это функция, но значение функции - это уже конкретно число. Есть определённый интеграл - это число, но это число не значения (первообразной) функции, в разность значений в двух точках, а я хочу найти значение в одной очке. Да и к тому же я исхожу из того, что я как бы не знаю исходного уравнения (первообразной) функции, у меня есть только уравнение производной и формула с интегралом.
Вот я как раз наглядно продемонстрировал то, в чём кроется моё непонимание неопределённого интеграла. Если с отпрядённым интегралом более или менее понятно - это предел интегральных сумм, мы ищем площадь, поэтому там оправдан знак интеграла как видоизмененный знак суммы, также расставлены пределы интегрирования, то как понимать знак интеграла в неопределённом интеграле - что я там "суммирую", совершенно неясно.
Если вернуться к задаче о нахождении для (первообразной) функции её значения, то если просто подставить в формулу значение $x_0$, получатся неверные результаты:
$f_1(x_0) + C_1 = 0$: $f_1(1) + (-1) = 0 \Rightarrow f_1(1) = 1$
$f_2(x_0) + C_2 = \int dx$: $f_2(1) + 0 = \int dx$ \Rightarrow f_2(1) = \int dx$
$f_3(x_0) + C_3 = \int 2x_0dx$: $f_3(1) + 0 = \int 2 \cdot1 dx \Rightarrow f_3(1) = \int 2dx$
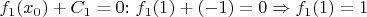
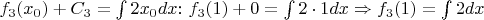
Если попытаться использовать определённый интеграл для одной точки $x_0 = 1$, то тоже получатся неверные результаты:
$f_1(x_0) + C_1 = 0$: $f_1(1) + (-1) = 0 \Rightarrow f_1(1) = 1$
$f_2(x_0) + C_2 = \int\limits_1^1 dx$: $f_2(1) + 0 = \int\limits_1^1 dx$ \Rightarrow f_2(1) = \int\limits_1^1t dx = 0$
$f_3(x_0) + C_3 = \int\limits_1^1 2x_0dx$: $f_3(1) + 0 = \int\int\limits_1^1 2 \cdot1 dx \Rightarrow f_3(1) = \int\limits_1^1 2dx = 0$
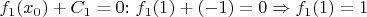
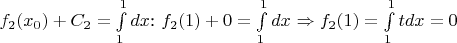
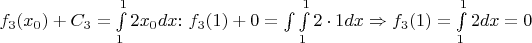
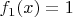
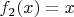
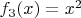
Если вспомнить, что исходные функции были $f_1(x)=1$, $f_2(x)=x$ и $f_3(x)=x^2$, то значения этих функций в точке $x_0 = 1$ должны быть быть, соответственно:
$f_1(x_0) = 1$: $f_1(1) = 1$
$f_2(x_0) = x_0$: $f_2(1) = 1$
$f_3(x_0) = x_0^2$: $f_3(1) = 1^2 = 1$
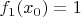
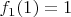
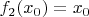
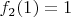
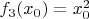
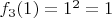
Вопросы:
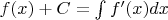
Вопрос 1: как я могу формально прийти к формуле $f(x) + C = \int f'(x)dx$ по аналогии с формулой, полученной для производной $f'(x) = \lim\limits_{\Delta x \rightarrow 0} \frac{f(x+\Delta x)-f(x)}{\Delta x}$?
Например, у меня есть уравнение функции $f(x) = x^2$, у могу из него получить уравнение производной:
$f'(x) = \lim\limits_{\Delta x \rightarrow 0} \frac{f(x+\Delta x)-f(x)}{\Delta x} = \lim\limits_{\Delta x \rightarrow 0} (2x-\Delta x)= 2x$
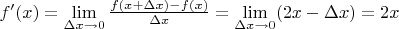
А теперь у меня есть уравнение производной: $f'(x) = 2x$, а я хочу из него получить уравнение (первообразной) функции (с точностью до константы), но не понимаю, как это сделать.
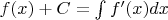
Вопрос 2: как мне использовать формулу $f(x) + C = \int f'(x)dx$ для поиска значений (первообразной) функции?

[Combat Zone]

Solaris86 в сообщении #1709296 писал(а):

Если вернуться к задаче о нахождении для (первообразной) функции её значения, то если просто подставить в формулу значение $x_0$, получатся неверные результаты:
$f_1(x_0) + C_1 = 0$: $f_1(1) + (-1) = 0 \Rightarrow f_1(1) = 1$
$f_2(x_0) + C_2 = \int dx$: $f_2(1) + 0 = \int dx$ \Rightarrow f_2(1) = \int dx$
$f_3(x_0) + C_3 = \int 2x_0dx$: $f_3(1) + 0 = \int 2 \cdot1 dx \Rightarrow f_3(1) = \int 2dx$
Если попытаться использовать определённый интеграл для одной точки $x_0 = 1$, то тоже получатся неверные результаты:
$f_1(x_0) + C_1 = 0$: $f_1(1) + (-1) = 0 \Rightarrow f_1(1) = 1$
$f_2(x_0) + C_2 = \int\limits_1^1 dx$: $f_2(1) + 0 = \int\limits_1^1 dx$ \Rightarrow f_2(1) = \int\limits_1^1t dx = 0$
$f_3(x_0) + C_3 = \int\limits_1^1 2x_0dx$: $f_3(1) + 0 = \int\int\limits_1^1 2 \cdot1 dx \Rightarrow f_3(1) = \int\limits_1^1 2dx = 0$
Если вспомнить, что исходные функции были $f_1(x)=1$, $f_2(x)=x$ и $f_3(x)=x^2$, то значения этих функций в точке $x_0 = 1$ должны быть быть, соответственно:
$f_1(x_0) = 1$: $f_1(1) = 1$
$f_2(x_0) = x_0$: $f_2(1) = 1$
$f_3(x_0) = x_0^2$: $f_3(1) = 1^2 = 1$

Что-то очень странное вы тут пишете.
Может, объясните, как вы сами это понимаете, на примере строчки номер три оттуда и оттуда?

Неопределенный интеграл - это очень простая штука. Это семейство всех первообразных на том множестве, где вы его считаете.
Функция $F$ называется первообразной $f$, если $F'(x)=f(x)$ на всей области определения.

Чтобы посчитать значение любой функции в точке (в т.ч. первообразной), нужно сперва знать функцию. Поэтому вы сначала считаете первообразную, потом смотрите ее значение в точке. Менять местами эти два действия нельзя, получится бессмыслица.
Точно так же получится бессмыслица, если вдруг при вычислении производной $y'(1)$ кто-то будет считать сперва $y(1)$, а потом дифференцировать полученное число.

Уравнение первообразной и уравнение производной - так не говорят. Слова "уравнение" тут лишние. Просто "производная и первообразная". Еще замечания нужны? Они есть, но пока и так много.

Solaris86 в сообщении #1709296 писал(а):

Вопрос 1: как я могу формально прийти к формуле $f(x) + C = \int f'(x)dx$

По определению первообразной (см. выше).

[Solaris86]

Combat Zone в сообщении #1709298 писал(а):

Что-то очень странное вы тут пишете.
Может, объясните, как вы сами это понимаете, на примере строчки номер три оттуда и оттуда?

Да, я написал некорректные выражения. Я сразу оговорился, что получаются неверные результаты. Я просто попытался поэкспериментировать с формулами и посмотреть, что получится.

Combat Zone в сообщении #1709298 писал(а):

Чтобы посчитать значение любой функции в точке (в т.ч. первообразной), нужно сперва знать функцию. Поэтому вы сначала считаете первообразную, потом смотрите ее значение в точке. Менять местами эти два действия нельзя, получится бессмыслица.

Вот-вот, как раз подошли к сути вопроса: получается, что интегрирование - это не только действие, обратное дифференцированию, но и действие несамостоятельное, вторичное по отношению к дифференцированию. То есть мы знаем формулы для дифференцирования, а интегрируем, просто как бы "проходясь" по формуле дифференцирования в обратную сторону.
Получается:
1. Если известна $f(x)$, неизвестна $f'(x)$, то найти найти $f'(x)$ можно.
2. Если известна $f'(x)$, неизвестна $f(x)$, то найти найти $f(x)$ (с точностью до константны) нельзя.
Так выходит?
Тогда формула

Combat Zone в сообщении #1709298 писал(а):

$f(x) + C = \int f'(x)dx$

также бессмысленна, как и мои рассуждения выше.
Ну вот как нас учат вычислять определённый интеграл:
$\int\limits_{x_1}^{x_2} f'(x)dx = f(x)|_{x_1}^{x_2}= f(x_2)-f(x_1)$
Например:
$\int\limits_1^2 2xdx = x^2 |_1^2 = 2^2 - 1^2 = 3$
Для производной и первообразной тогда нужно оставить только одно выражение:
$f'(x) = \lim\limits_{\Delta x \rightarrow 0} \frac{f(x+\Delta x)-f(x)}{\Delta x}$
У нас есть выражение для дифференциалов:
$df(x) = f'(x)dx$.
Мы интегрируем это выражение и получаем выражение для интегралов:
$\int df(x) = \int f'(x)dx$.
Это всё. А дальше снова затык: как получить, что $\int df(x) = f(x) + C$, если у нас нет формулы - аналитического выражения - для вычисления первообразной на основе производной, о чём я и написал выше?
Да и сама формула выглядит странно: интеграл дифференциала - это же по сути сумма приращений, но:
1. Не оговорены границы суммирования (или по умолчанию понимается, что тут сумма на всей области определения?).
2. Не говорено, чему равны эти приращения - они имеют конечные значения или являются бесконечно малыми, так как в матанализе какая-то неопределённость с толкованием дифференциалов: то где-то у нас $dx = \Delta x$ при $\Delta x \rightarrow 0$, то есть $dx$ - это бесконечно малая величина и $df'(x)$, соответственно, тоже бесконечно малая величина, если мы имеем дело с вычислением производной, то где-то у нас $dx$ и $df(x)$ - уже вообще любое конечное число, если мы имеем дело с приближёнными вычислениями...

[Combat Zone]

Solaris86 в сообщении #1709301 писал(а):

Вот-вот, как раз подошли к сути вопроса: получается, что интегрирование - это не только действие, обратное дифференцированию, но и действие несамостоятельное, в вторичное по отношению к дифференцированию.

А логарифм вас не смущает? Или арксинус? Когда это действие, обратное другому, и именно так и определяется? Как обратное?
И ничего, пишут $\log_2{10}$ и не пугаются. Вернее, пугаются, но до поры. Хотя что это такое, не сказать, без того, что мы получили число такое, что если 2 возвести в эту степень, получится 10.

Solaris86 в сообщении #1709301 писал(а):

Тогда формула Combat Zone в сообщении #1709298

писал(а):
$f(x) + C = \int f'(x)dx$ также бессмысленна, как и мои рассуждения выше.

Вот тут не надо было на меня ссылаться, потому что фундаментальная теорема анализа (она же теорема Ньютона-Лейбница) требует выполнения ряда условий на f.
Когда рассказывают ее на первом курсе или гуманитариям, об этих условиях упоминать даже противопоказано. Упоминают более жесткие.

-- 15.11.2025, 10:35 --

Solaris86 в сообщении #1709301 писал(а):

Мы интегрируем это выражение и получаем выражение для интегралов:
$\int df(x) = \int f'(x)dx$.
Это всё. А дальше снова затык: как получить, что $\int df(x) = f(x) + C$, если у нас нет формулы - алгебраического выражения - для вычисления первообразной на основе производной, о чём я и написал выше?

Вроде уже поговорили об этом. По определению. Вы хотите доказать, что
$\int f'(x)dx = f(x)+C$.
То есть что всякая функция $f(x)+C$ является первообразной $f'(x)$.
То есть должно выполняться $(f(x)+C)'=f'(x)$. Дальше сами, пожалуйста.

[Евгений Машеров]

Просто надо понимать, что неопределённый интеграл это не функция. Это семейство функций, зависящее от параметра. Поэтому говорить о "численном значении неопределённого интеграла" это примерно то же, что говорить о "численном значении роста членов семьи". Когда этот параметр, постоянная интегрирования, задан - это уже функция, имеющая определённое значение. До того - не функция, хотя запись выглядит, как функция.

[Combat Zone]

Евгений Машеров
Судя по тексту, у товарища и понятие первообразной будет вызывать протесты на том же основании, ввиду "вторичности". Так что собака порылась не только в НИ.

[Solaris86]

Combat Zone в сообщении #1709302 писал(а):

А логарифм вас не смущает? Или арксинус? Когда это действие, обратное другому, и именно так и определяется? Как обратное?
И ничего, пишут $\log_2{10}$ и не пугаются. Вернее, пугаются, но до поры. Хотя что это такое, не сказать, без того, что мы получили число такое, что если 2 возвести в эту степень, получится 10.

А почему меня должны смущать логарифм или арксинус?
А. Степень
1. Прямое действие - нахождение степени: $c = a^b$
2.1 Обратное действие 1 - нахождение основания степени: $a = \sqrt[b]{c}$
2.2 Обратное действие 2 - нахождение показателя степени: $b = \log_a{c}$
Б. Синус угла $\alpha$ как отношение противолежащего катета $a$ к гипотенузе $c$:
1. Прямое действие - нахождение значения синуса для известного значения угла $\sin \alpha = \frac {a}{c}$
2. Обратное действие - нахождение значения угла для известного значения синуса $\arcsin \frac {a}{c} =\alpha$
Здесь везде аналитические выражения, которые можно применять, подставляя численные значения вместо букв и выполняя соответствующие операции.
В случае с неопределенным интегралом так не получается (выше я попробовал):
$\int df(x) = \int f'(x)dx$
$\int df(x) = f(x) + C$
$ f(x) + C = \int f'(x)dx$
Эти формулы какие-то странные в том смысле, что ими напрямую нельзя пользоваться без перехода к первообразной.
Для сравнения: формулой с дифференциалами $df(x) = f'(x)dx$ почему-то можно спокойно пользоваться.
Возьмём опять же функцию $f(x) = x^2$. Её производная $f'(x) = 2x$.
А теперь поэкспериментируем со всеми выражениями, взяв $x_0 = 1$, $dx = 0.1$ и $C = 0$:
1. $df(x_0) = f'(x_0)dx$: $df(1) = 2 \cdot 1 \cdot 0.1 = 0.2$ - приближённые вычисления
2. $\int df(x_0) = \int f'(x_0)dx$: $\int 0.2 = \int (2 \cdot 1 \cdot 0.1) = \int 0.2$ - бессмыслица
3. $\int df(x_0) = f(x_0) + C$: $\int 0.2 = 1^2 = 1$ - бессмыслица
4. $ f(x_0) + C = \int f'(x_0)dx$: $1 = \int 0.2$ - бессмыслица
Я это к тому, что выражения с неопределённым интегралом нельзя использовать как аналитические выражения, а выражение с дифференциалами можно. Это и вызывает непонимания. Зачем выражения с неопределёнными интегралами вообще нужны вообще нужны в таком виде? Я искал в книгах по истории матанализа, откуда появился неопределённый интеграл, но не нашёл ответа, там больше всё про определённый интеграл как следствие задач на нахождение площадей и объёмов... У меня складывается впечатление, что сначала появился определённый интеграл как конкретный рабочий инструмент, а потом уже из него выделился неопределённый интеграл как какая-то абстрактная конструкция, внешне сходная с определённым интегралом, но которую нельзя использовать ни для чего вообще...

-- 15.11.2025, 12:49 --

Combat Zone в сообщении #1709302 писал(а):

Когда рассказывают ее на первом курсе или гуманитариям, об этих условиях упоминать даже противопоказано. Упоминают более жесткие.

Что за условия и за более жёсткие условия?

Combat Zone в сообщении #1709302 писал(а):

Дальше сами, пожалуйста.

Эти доказательства понятны.

Евгений Машеров в сообщении #1709303 писал(а):

Когда этот параметр, постоянная интегрирования, задан - это уже функция, имеющая определённое значение.

Тогда, может быть, для заданной постоянной интегрирования можно как-то получить аналитическое выражения для нахождения первообразной, если известная производная?

Combat Zone в сообщении #1709305 писал(а):

Судя по тексту, у товарища и понятие первообразной будет вызывать протесты на том же основании, ввиду "вторичности". Так что собака порылась не только в НИ.

Первообразная не вызывает никаких протестов.

[Someone]

Solaris86 в сообщении #1709308 писал(а):

Тогда, может быть, для заданной постоянной интегрирования можно как-то получить аналитическое выражения для нахождения первообразной, если известная производная?

А Вы где учитесь-то? Каким учебником пользуетесь? Что, совсем никаких методов получения аналитического выражения для первообразной Вам не показывали?

[Евгений Машеров]

Solaris86 в сообщении #1709308 писал(а):

Тогда, может быть, для заданной постоянной интегрирования можно как-то получить аналитическое выражения для нахождения первообразной, если известная производная?

Конечно, можно! $+C$, только в качестве C подставляется это самое Ваше "известное значение"

[Combat Zone]

Solaris86 в сообщении #1709308 писал(а):

Первообразная не вызывает никаких протестов.

Это хорошо. Так чему равна первообразная функции $f(x)=x^3$?

[Solaris86]

Someone в сообщении #1709310 писал(а):

Solaris86 в сообщении #1709308 писал(а):

Тогда, может быть, для заданной постоянной интегрирования можно как-то получить аналитическое выражения для нахождения первообразной, если известная производная?

А Вы где учитесь-то? Каким учебником пользуетесь? Что, совсем никаких методов получения аналитического выражения для первообразной Вам не показывали?

Я сейчас уже нигде не учусь. Сейчас понадобилось освежить знания по матанализу и решил заодно выяснить все вопросы, которые возникали раньше при изучении матанализа. Я разные учебники использовал: и Письменного, и Фихтенгольца, и Зорича.
По поводу получения аналитического выражения для первообразной - нигде ни разу не видел, его и пытаюсь найти. Думаю, что вы под этой фразой понимаете не то, что имею в виду я... Чтобы мы понимали эту одинаково, напишу пример.
Вот пусть есть функция $f(x) = x^2$. У меня есть задача - найти множество касательных к ней.
Решаю задачу в 2 этапа:
Этап 1. Нахожу формулу для расчёта тангенса угла наклона касательной в любой точке, то есть производную:
$f'(x) = \lim\limits_{\Delta x \rightarrow 0} \frac{f(x+\Delta x)-f(x)}{\Delta x} = \lim\limits_{\Delta x \rightarrow 0} (2x-\Delta x)= 2x$
Этап 2. Нахожу формулу касательной в любой точке графика функции $f(x) = x^2$
$y_\text{кас}(x_0)-y_0 = f'(x_0) \cdot (x-x_0) \Rightarrow y_\text{кас}(x_0) = f'(x_0) \cdot (x-x_0) - y_0 = f(x_0) \cdot x - (f(x_0) \cdot x_0 + y_0)$
Задача решена, я нашёл уравнения всего множества касательных.
Теперь у меня обратная задача - найти исходную функцию, имея уравнение всего множества касательных к ней.
Я должен получить аналитическое выражение, которое начинается с $f(x)$ и заканчивается на $x^2 + C$:
$f(x) = ... = x^2 + C$
В учебниках же при интегрировании мне просто предлагает выполнить последовательность действий, обратную дифференцированию.
https://www.dropbox.com/scl/fi/jx4m7e1c ... 5fp4v&dl=0
А я же хочу узнать, как с помощью аналитического выражения в обратном порядке проделать эту последовательность действий шаг за шагом, чтобы из производной получить первообразную (при этом не пользоваться уже известными таблицами интегралов).

-- 15.11.2025, 17:14 --

Combat Zone в сообщении #1709312 писал(а):

Solaris86 в сообщении #1709308 писал(а):

Первообразная не вызывает никаких протестов.

Это хорошо. Так чему равна первообразная функции $f(x)=x^3$?

$F(x) = \frac {x^4}{4} + C$
Но это опять же взято из таблицы интегралов, а не выведено последовательно.

[dgwuqtj]

Solaris86 в сообщении #1709308 писал(а):

А почему меня должны смущать логарифм или арксинус?

Попробуйте посчитать $\arcsin \frac 1 2$, не пользуясь таблицей синусов, а с помощью некоего "аналитического выражения".

[Solaris86]

dgwuqtj в сообщении #1709337 писал(а):

Solaris86 в сообщении #1709308 писал(а):

А почему меня должны смущать логарифм или арксинус?

Попробуйте посчитать $\arcsin \frac 1 2$, не пользуясь таблицей синусов, а с помощью некоего "аналитического выражения".

Ну, как вариант через ряд Тейлора, нет?
Но тут же речь про иной: арксинус - это некий оператор, который на входе получает значение синуса, а на выходе выдает значение угла. Само значение угла мы считаем через ряд Тейлора.
В случае с производной и неопределённым интегралом получается, что аналитическое выражение для нахождение производной есть, а для нахождения первообразной его нет. Я имею в виду сами последовательные выкладки и рассуждения. Нам просто говорится: возьми производную и произведи действия, обратные дифференцированию в смысле именно из таблицы производных сделай таблицу интегралов.

[Combat Zone]

Solaris86 в сообщении #1709343 писал(а):

Ну, как вариант через ряд Тейлора, нет?

Это не тот ли самый, где в качестве свободного члена стоит в аккурат $\arcsin \frac 1 2$?

... давайте с чем-то одним разберемся. С арксинусом, например. А то какой-то салат.

[dgwuqtj]

Solaris86 в сообщении #1709343 писал(а):

Ну, как вариант через ряд Тейлора, нет?

А чем тогда не устраивает вычисление первообразной через определённый интеграл, как предел интегральных сумм?