Здравствуйте, уважаемые участники форума!
Хочу представить на ваш суд и обсуждение математическую конструкцию, которая демонстрирует ряд любопытных свойств и приводит к нетривиальной открытой проблеме. Работа является результатом совместного исследования с моим научным партнером.
Если бы эту задачу ставил Диофант Александрийский, она могла бы звучать так:
Цитата:
Задача о неуловимом решенииЯ ищу пятерку целых чисел вида
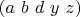
. Эти числа должны удовлетворять уравнению:

при следующих суровых условиях:
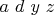 — целые большие единицы;
— целые большие единицы; равно 0 или 1;
равно 0 или 1; не превосходит
не превосходит  ;
;- И
 , и
, и  должны быть больше, чем величина
должны быть больше, чем величина  .
.
Я испробовал все известные мне методы и перебрал все числа

до 5000, но не нашел ни одного решения и начинаю подозревать, что это уравнение не имеет решений в целых числах.
Проблема: Либо докажите, что решений не существует, либо явите мне первую пятерку чисел, которая удовлетворяет всем условиям. Тот, кто решит эту задачу, постигнет глубокую истину о природе чисел, порожденных этой формой.
А вот современное описание проблемы.
1. ВведениеПусть

— положительное целое число. Пусть

равно 0 или 1 и
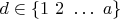
. Определим следующие функции:
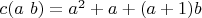
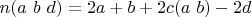
Рассмотрим целое число (кандидат в простые):
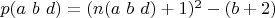
Для каждого кандидата
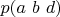
определим "решето"

как выполнение следующего условия: для всех целых

в диапазоне
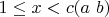
не выполняется сравнение:
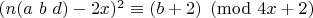
Обозначим через
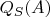
множество чисел
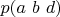
с параметром
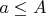
. Для всех элементов этого множества условие

истинно.
Теорема 1.Пусть
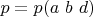
.
(a) Если

простое то

истинно.
(b) Если

составное и имеет простой делитель

с
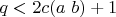
то

ложно.
Мы провели компьютерную проверку для всех параметров вплоть до
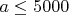
. Эта проверка охватывает более 25 миллионов (25005000) кандидатов. В множестве
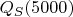
был обнаружен 2427441 простых чисел и ни одного составного.
Следовательно любой гипотетический составной элемент

должен удовлетворять очень сильному условию: все его простые делители

должны быть не меньше

.
Открытая проблема. Доказать или опровергнуть: для любых параметров

(при

), если
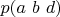
составное то оно имеет простой делитель
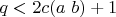
.
2. Доказательство Теоремы 1Лемма 2.1. Пусть
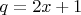
для целого

. Утверждение

эквивалентно утверждению
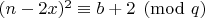
.
Доказательство. Тождество
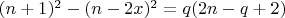
показывает что разность квадратов делится на

.
 Лемма 2.2.
Лемма 2.2. Для всех допустимых параметров выполняется
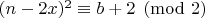
.
Доказательство. По построению
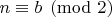
и
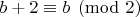
поэтому
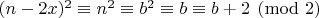
.
 Лемма 2.3.
Лемма 2.3. Для

справедливо

.
Доказательство. При фиксированных

минимум

достигается при

. Анализ полученного выражения показывает что оно строго больше

для всех

.
 Доказательство Теоремы 1.
Доказательство Теоремы 1.(а) Предположим

простое но

ложно. Тогда для некоторого

в диапазоне
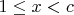
имеем
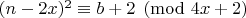
. Пусть
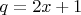
. Сравнение верно и по модулю

. По Лемме 2.1 это эквивалентно

то есть

что влечет
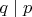
. Так как

простое должно быть

. Но

а по Лемме 2.3
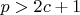
. Получаем противоречие.
(b) Пусть

— простой делитель

с

. Из Леммы 2.2 следует, что

нечетно значит

тоже нечетно. Положим
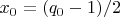
тогда
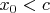
. Из
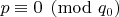
и Леммы 2.1 следует
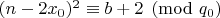
. По Лемме 2.2 также имеем
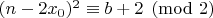
. По Китайской теореме об остатках эти два сравнения объединяются в

то есть
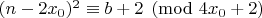
. Это противоречит условию

.
 3. Вычислительные Результаты
3. Вычислительные РезультатыОбозначим через
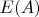
множество составных чисел
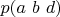
с
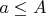
, для которых

истинно ("выжившие составные").
Таблица 1. Результаты компьютерного поиска для
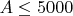
.
Код:
+--------+------------+-----------------+--------------------+
| A | Кандидатов | Найдено простых | Выживших составных |
| | | |Q_S(A)| | |E(A)| |
+--------+------------+-----------------+--------------------+
| 100 | 10100 | 1886 | 0 |
| 1000 | 1001000 | 120921 | 0 |
| 3000 | 9003000 | 907521 | 0 |
| 5000 | 25005000 | 2427441 | 0 |
+--------+------------+-----------------+--------------------+
Основное наблюдение: Для всех
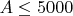
множество выживших составных чисел пусто:
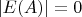
.
Анализ плотности: Наблюдаемая плотность простых
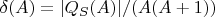
составляет
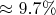
при
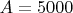
. Для сравнения естественная плотность простых для чисел порядка

составляет примерно

.
4. Формулировка Открытой ПроблемыГипотеза 4.1. Утверждается что для любых параметров


равно 0 или 1 и
![$d \in [1\ a]$ $d \in [1\ a]$](https://dxdy-02.korotkov.co.uk/f/1/6/5/16595e4a19976fb32ff65dd5ca80ca5e82.png)
если число
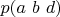
составное то оно имеет простой делитель
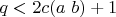
.
Диофантова формулировка. Гипотеза 4.1 эквивалентна утверждению что следующая диофантова система не имеет решений в целых числах:
Это ставит нашу проблему в контекст сложных задач о целочисленных решениях полиномиальных уравнений.
Приглашаю всех желающих к обсуждению, критике и поиску доказательства или контрпримера.
Исходный код для верификации выложен на GitHub:
https://github.com/ASSA-NI-ATOM/parametric-sieveDOI препринта:
https://doi.org/10.5281/zenodo.17567681Цитата: