Dendr - спасибо за задачу! Если вы вдруг следите там (за этой задачей в ежемесячнике) и они публикуют решения, дайте знать!
В этой теме, идейно, усилиями нескольких участников, в том числе Вашими

, задача уже решена.
Но, к сожалению, на финальном этапе посчитана одна из вероятностей неверно. Для удобства, собираю все части решения в одном сообщении
и исправляю ошибку в ответе. Это уже сделать легко, зная сам ответ.
Итак, вот начало:
Давайте для начала посмотрим, какие конфигурации у нас могут быть после первого броска. Считаем за аксиому, что первым броском мы должны бросать все кубики.
Всего возможны

вариантов, которые разбиваются на 7 возможных классов (подсчитано с помощью компьютерной программы, ибо плохо умею по-другому):
1) Все числа разные (ABCDE) — 720 исходов
2) Три числа разные, два одинаковые (AABCD) — 3600 исходов
3) Два числа разные, три одинаковые (AAABC) — 1200 исходов
4) Одно число, два одинаковых, и ещё два одинаковых (AABBC) — 1800 исходов
5) Два одинаковых и ещё три одинаковых (AAABB) — 300 исходов
6) Одно число и четыре одинаковых (AAAAB) — 150 исходов
7) Все числа одинаковые (AAAAA) — 6 исходов
Немедленный успех (один бросок) — это классы 5) и 7), матожидание 1.
Исходы можно вычислять без компьютера, в дальнейшем пригодится. Например,
4) Одно число, два одинаковых, и ещё два одинаковых (AABBC) — 1800 исходов
У нас есть

различных чисел. Первые два

могут быть реализованы выбором одного числа из

и заполнением в упорядоченной пятиклеточной строке

двух клеток; число способов
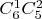
. Далее

реализуется
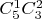
способами, a

реализуется
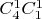
способами. Заметим, что мы насчитали вдвое больше способов, чем нужно. Поскольку в раскладке
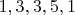
-- поди разберись кто есть A, а кто B. Мы посчитали его и как
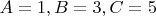
, и как
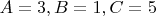
. Перемножаем все способы и делим на

:

-- с ответом
worm2 совпадает.
Вторая часть решения:
Тут лучше считать с конца, сначала с 4 отложенными кубиками, потом с 3, потом с 2, потом уже из начальной позиции (откладывать 1 кубик смысла нет).
Пока что выяснились следующие матожидания в зависимости от уже отложенных кубиков:
AAAA - 6
AAAB - 6
AABB - 3
AAA - 6
AAB -
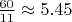
(откладываем B если попадется)
AA -
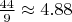
(откладываем BB)
AB -
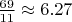
(откладываем AB если получится, иначе откладываем только A или только B)
Очень красивая идея!
Но, к сожалению, именно тут закралась одна досадная ошибка. (Оффтоп)
Мне мерещатся всюду ошибки, так как я не умею читать условие и чересчур доверяю ИИ

, обозначим это ожидание

.
Конечно, ошибка перекочевала и в 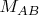 .
. При этом,
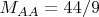
посчитано верно, я это перепроверил в сообщении
https://dxdy.ru/post1708016.html#p1708016. Значит, уважаемый
12d3 считал похожим способом. Жаль, что я тогда поленился перепроверить

, была ночь.
Как итог, состояние 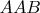 так и осталось недооценённым. Лучше бы вообще не влезал, раз условие не научился читать и думаю, что ИИ читает его внимательнее.
так и осталось недооценённым. Лучше бы вообще не влезал, раз условие не научился читать и думаю, что ИИ читает его внимательнее.И вот, наконец, третья часть -- это численная проверка, которую выполнил уважаемый
wrest,
не поинтересовавшийся у ИИ понял ли тот его и условие 
Его результат прямо кричит: "что же вы, эдакие и сякие, не хотите пересчитать

". Собственно, вот пересчёт:
из состояния
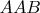
за один ход выигрываем, если
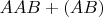
или

;
переходим в пару различных дублей (там маленькое ожидание), если
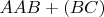 или если
или если 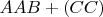 (тогда придётся вытаскивать из уже отложенных
(тогда придётся вытаскивать из уже отложенных  , чего нельзя по условию)
, чего нельзя по условию) Добавлено в 12:20 03.11.2025 ;
в остальных случаях остаёмся в
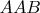
, так как ожидание у состояния
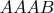
равно

, а состояние

для любителей кидать кубик долго

Тогда

находим из формулы:
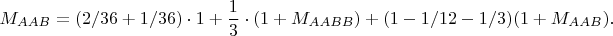
Поскольку
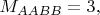
то
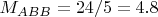
. Видно, что
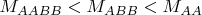
. Отсюда стратегия
(она будет верная, только если кубики из отложенных снова можно вовлекать в игру)Рекомендации
AAAAA - держать все (победа)
AAAAB - держать AAB
AAABB - держать все (победа)
AAABC - держать AAB
AABBC - держать AABB
AABCD - держать AAB
ABCDE - держать A
Только добавлю, что из
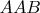
, если нет победы после броска, но есть переход в два различных дубля, то идём в дубли. И следующее замечание тоже верное:
По случаю "выпали все разные", мне как-то кажется, что перебросить все или перебросить 4 - нет разницы.
Формула для расчёта минимального ожидания числа бросков до победы с начала игры
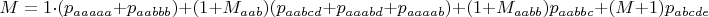
Буквой

с индексами обозначены вероятности состояний после первого броска.
Что даёт
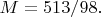 Этот результат будет правильным, только если кубики из отложенных снова можно вовлекать в броски.
Этот результат будет правильным, только если кубики из отложенных снова можно вовлекать в броски.(Оффтоп)
Уважаемый
worm2 начал решение с введения удобных обозначений,
12d3 продолжил её решать и решил,
wrest с помощью ИИ поставил другую задачу с возвращаемыми кубиками и решил её численно, я помог разобраться в расхождении условий задач
