Вероятность исхода
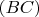
равна
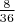
, а не

, разве нет?
Да.
Когда сидел ночью и обдумывал результат ИИ, в какой-то момент показалось (часу во втором), что в дубли можно перейти ещё и так
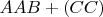
(про это забыл сказать в сообщении). Тогда, вероятность
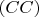
равна 4/36, а вероятность
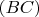
или
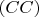
равна
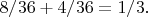
Но сейчас утро (начало первого

) и теперь видно, что в случае
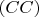
нам потребуется вытащить

из состояния
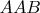
для продолжения игры. Надо обратиться к условию, в котором сказано:
После каждого броска вы можете отложить любое количество кубиков, возможно все, в сторону - тем самым исключая их из последующих бросков - а потом бросить остальные повторно.
Решение
12d3 не содержит ошибок. ИИ пытается хитрить, вновь вовлекая в игру уже отложенные кубики, либо недопонял условие от
wrest.
(Оффтоп)
12d3, извините. Предыдущее сообщение исправил. Удалять его не буду, так как в обоих постановках, с возвращаемыми или нет кубиками, задача выглядит содержательной.