Вот у нас есть отрезок в

.
В

?
он замкнут по всей своей длине? Или замкнуты только его концы?
Как было верно сказано, нет таких понятий. Отрезок - замкнут, концы ему принадлежат.
И что произойдет с точкой отрезка, если мы присоединим к ней n отрезков, а затем отделим от нее n интервалов той же длины?
Смотря что значит "присоединим". Если в смысле объединения (

), то точки, принадлежащие обоим множествам, при объединении этих множеств не "удваиваются". Например,
![$[0,1]\cup[1,2]=[0,2]$ $[0,1]\cup[1,2]=[0,2]$](https://dxdy-01.korotkov.co.uk/f/c/d/f/cdf663f26a48ac9d503ef6e7937a483982.png)
. Если "удалим" в смысле разности множеств (

), то, например,
![$[0,2]\backslash(1,2]=[0,1]$ $[0,2]\backslash(1,2]=[0,1]$](https://dxdy-03.korotkov.co.uk/f/e/8/4/e84c735454ebf13a1dbac8e96e2120aa82.png)
;
![$[0,2]\backslash[1,2]=[0,1)$ $[0,2]\backslash[1,2]=[0,1)$](https://dxdy-01.korotkov.co.uk/f/c/7/7/c7775300f1f2406d1c6b4d01a15deae582.png)
. Таким образом,
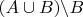
не обязательно равно

.
Грубо говоря, по самому своему смыслу множество содержит каждый свой элемент "только один раз"; вообще не определено, что значит "содержать какой-то элемент несколько раз".
Почему принято считать, что отрезок при делении делится на 2 отрезка, а не на полуинтервал и отрезок
Не принято так считать. Если точка

находится внутри отрезка
![$[a,b]$ $[a,b]$](https://dxdy-04.korotkov.co.uk/f/f/e/4/fe477a2781d275b4481790690fccd15f82.png)
, иногда бывает удобно рассмотреть отрезки
![$[a,c]$ $[a,c]$](https://dxdy-02.korotkov.co.uk/f/5/0/8/508064867c3a35e2e8ddbdee8c1d7f4b82.png)
и
![$[c,b]$ $[c,b]$](https://dxdy-03.korotkov.co.uk/f/2/9/f/29f5f7bb6633454c5f66c579cbb5322382.png)
, иногда полуинтервал
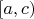
и отрезок
![$[c,b]$ $[c,b]$](https://dxdy-03.korotkov.co.uk/f/2/9/f/29f5f7bb6633454c5f66c579cbb5322382.png)
. Как удобно и как нужно для конкретной задачи, так и рассматривают. "Делится" - не строгий математический термин, а скорее жаргон - в разных контекстах он может пониматься по-разному.
-- 30.10.2025, 18:05 --При этом в стандартной топологии на

отрезок не является ни замкнутым, ни открытым множеством. В

он замкнут.
Что Вы такое говорите. Отрезок замкнут и в

, и в

. Вот интервал - действительно не открыт и не замкнут в

, хотя открыт в

.