Так ничего не очевидно и ничего не понятно в этих формализмах
Откройте учебник матана за первый курс. Хотя тут вроде бы даже школьные обозначения, насколько я помню, в старших классах что-то на тему бесконечных сумм руками машут, этого вполне достаточно.
Если Вы хотите что-то спросить про бесконечные ряды - то нужно разобраться с тем, что это такое. До тех пор стоит ограничиться вопросами, которые помогут в этом разобраться, что-то другое только запутает.
И еще одна бесконечная последовательность с суммой равной 1:
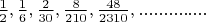
Тут непонятно, какой общий член. Но Вы можете хотя бы просто вместо букв подставить конкретные числа? Если нет - то повторите программу за примерно 5й класс прежде чем думать о рядах.