Спасибо!
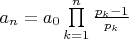
?
Да, правильно. Ещё можно убрать множитель

:
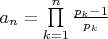
Оказывается, что
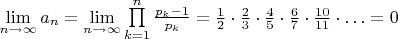
Еще непонятно как увидеть к чему стремится этот остаток в пределе. Неужели к 0?
Да. Как это увидеть? Я не умею это доказывать «с нуля», но знаю, как это вывести из известного факта, что
ряд обратных простых расходится:
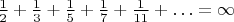
Каждый знаменатель уменьшим на

, от этого каждый член ряда станет больше, а потому
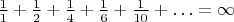
Следовательно,
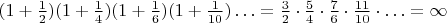
(попробуйте сами увидеть, как это получается из предыдущей формулы). А отсюда рукой подать до нашего произведения.
Спасибо. Вы все подробно разжевали. Все понял.
-- Вт окт 28, 2025 13:31:46 --(Оффтоп)
лежу сейчас с ковидом, с температурой 39
Выздоравливайте поскорее. Если не секрет, Вы прививались от ковида (когда-нибудь)?
(Оффтоп)
Спасибо, критическую фазу уже прошел, температура пошла на спад. Никогда не прививался от ковида. Чувствовал, что это зло. Каждый год болел в феврале 1 раз в легкой форме. Но в этом году заболел в октябре и не так легко все проходило. Лечусь народными средствами, чаи с травами, мед, варенья. Верю в теорию заговора, поэтому ничего хорошего от прививок, продуктов со штрихкодами из магазина и т.д. не ожидаю. Ну например, молоко можно привезти в магазин 1 раз в месяц и оно не испортится, но для этого надо добавить консервант, а можно привозить через день и оно будет на 3-й день скисать. Привозить раз в месяц выгоднее- меньше транспортных расходов, меньше испорченного, просроченного продукта и это дает больше прибыли или возможность снизить цену и потеснить конкурентов и т.д. Но цена этой прибыли - здоровье покупателей, которые едят консерванты. И примерно по такой схеме работает рыночная экономика и если посмотреть на США, например, то там этих продуктов здоровых и нет вовсе. Экономическая целесообразность и выгода выше здоровья человека. Ну а почему какая-то забота о здоровье человека и его генетике должна быть в прививках при таком подходе? Властьимущим и элитам важна стабильность экономики, чтобы продукты производились, прибыль шла, а генетика и здоровье- они на втором плане, а то и вовсе на противоположной стороне)))
-- 28.10.2025, 16:24 --Спасибо.