-64 вершины куба и почти эйлерова характеристика

[Altenter]

Здравствуйте.
Рассмотрим куб, сложенный из кубиковплотнейшим образом. Каждый кубик укладывается со своими ребрами гранями и вершинами. В узле, внутри куба сходятся 8 кубиков, а в узлах, которые являются вершинами кубика, 8×8=64 вершины. Ну, вынем мысленно кубик вместе с его вершинами из этой плотнейшей упаковки. Окажется, что к месту, где он должен быть, примыкает 56 вершин от соседних кубиков, а к месту каждой из его 8-ми вершин 56/8=7. Т.е. в плотнейшей кубической упаковке у вершины куба 7 соседей, что в принципе было и так очевидно и я зря забивал вам голову.

Теперь возьмем выдернем отдельный кубик, вместе с его ребрами, вершинами и гранями и рассмотрим его почти эйлерову характеристику. Для этого придется раздеть куб. Вот мы снимем с него 6 граней, но вместе с ними снимутся и 6×4=24 ребра. Но каждое ребро имеет по 2 итого 48 вершины и 6 граней имеют по 4 вершины 6×4=24. Итого, снимая грани, мы стянули с кубика и 24 ребра и 24+48=72 вершины. Но нам надо вернуть ему 12 ребер, чтобы у него их не осталось, но вместе с 12-ю ребрами ему вернутся и 24 вершины. Итого напротив нас кубик без граней и ребер лишь в одних трусах с восемью вершинами, а у нас -72+24=-48 его вершин.
И вот этот кубик с 8 вершинами получается отрицательный персонаж, т.к. равен он вместе со своими 8 вершинами - 48-ми вершинам. Ну чтож, снимем с кубика и трусы, вычтя из обеих частей равенства по 8 вершин и тут о чудо, с одной стороны равенства голый кубик, а с другой (-56) вершин. Но у кубика - то всего 8 вершин, а тут мы с него сняли 56. 56/8=7. Т.е. наш кубик оказался воришкой и каждая его вершина украла по 7 вершин от 7 соседей, пока находилась в плотной упаковке с ними.

Ну чтож, попробуем вывести на чистую воду и других, более матерых преступников, которые тоже промышляют воровством, но в плотную упаковку никогда не укладываются. Тетраэдр, не решена проблема его плотнейшей упаковки, поэтому он гуляет на свободе. Посмотрим что у него есть из одежды. Так, 4 грани, да в каждой из низ по 3 ребра итого 4×3=12 ребер, да в каждом ребре 2 вершины итого 24 вершины и в каждой из 4-х граней по 3 итого 12, т.е. сняли 4 грани, 12 ребер и 36 вершин. Граней стало у него 0, а вот по ребрам прошлись не слабо и переборщили, надо бы вернуть 6 ребер, чтобы их у него не осталось. Но вместе с ними вернется и 12 вершин. Итого тетраэдр в одних трусах с 4-мя вершинами равен -36+12=-24 вершинам. Ну вычтем как и с кубом из обеих частей равенства трусы и получим, что голый тетраэдр равен -28 вершинам. Т.е. и он у нас отрицательный персонаж. Поделим 28 на количество его голых вершин и получим, что на каждую свою вершину он тоже украл по вершине у 7-ми соседей. Т.е. в наиплотнейшей упаковке у вершины тетраэдра, как и у куба было тоже 7 соседей. Это мы знаем точно, потому, что если было бы больше, он украл бы у всех них вершину. А если было бы меньше, то мы бы и не обнаружили у него 28 ворованных вершин.
Ну, или по крайней мере тетраэдр в плотнейшей упаковке украл 28 вершин на свои 4 вершины.

И кстати, кубик, если у него конфисковать его вершины вместе с ворованными будет иметь (-64) вершины, а тетраэдр (-32 ).
Т.е. у этих плутишек под ворованными трусами одеты еще и свои. И только сняв 64 трусов с куба и 32 с тетраэдра мы увидим их наготу.

[Altenter]

Подсчитал почти эйлерову характеристику для октаэдра, получилось -54 вершины, если поделить на 6 его вершин, то получится по 9 вершин от соседних октаэдров в плотнейшей упаковке. Т.е. у тетраэдра и куба по 7, а у октаэдра- 9.
Теперь вопрос, как это может помочь в поисках плотнейшей упаковки? Или хотя бы можно ли как-то с помощью этого расчитать процент заполняемости пространства этими правильными многогранниками?

[Altenter]

Прикинул почти эйлерову характеристику для:
додекаэдра она равна -140 вершин, $\frac{-140}{20}=-7$ вершин на вершину,
икосаэдра она равна -120 вершин, $\frac{-120}{12}=-10$ вершин на вершину.

[Mikhail_K]

Altenter
Непонятно, в чём смысл всех этих вычислений. Можно их написать с формулами и без метафор?

Altenter в сообщении #1705390 писал(а):

Вот мы снимем с него 6 граней, но вместе с ними снимутся и 6×4=24 ребра. Но каждое ребро имеет по 2 итого 48 вершины и 6 граней имеют по 4 вершины 6×4=24. Итого, снимая грани, мы стянули с кубика и 24 ребра и 24+48=72 вершины.

Это какие-то странные "правила игры", когда вершины считаются отдельно у каждого ребра (даже если какие-то из них совпадают) и ещё плюс к тому отдельно у каждой грани. Такие фразы тоже напускают туману:

Altenter в сообщении #1705390 писал(а):

Но нам надо вернуть ему 12 ребер, чтобы у него их не осталось

Если Вы хотите, чтобы Вас поняли, напишите всё нормально и в общем виде, а не на отдельных примерах. Вы ведь явно пишете что-то, что должно относиться сразу к многим видам многогранников. А то тут непонятно, делаете ли Вы вообще какое-то утверждение, и если да, то как его доказываете, а если нет, то к чему это всё.

(Оффтоп)

Пока больше всего мне эти манипуляции напоминают известную "загадку":

Ты берешь в долг у мамы 25 рублей, и у папы 25, всего у тебя 50 рублей.
Идешь в магазин и тратишь там ровно 45 рублей.
По дороге домой ты даешь в долг другу 3 рубля.
У тебя остается 2 рубля.
Ты приходишь домой, отдаешь долг маме - рубль и папе - рубль.
Теперь ты должен им по 24 рубля.
Итог: 24 + 24 равно 48, и 3 рубля тебе отдает друг, получается 51.
Вопрос - откуда взялся рубль если у тебя было 50?

Мораль: если складывать и вычитать что попало, то и получится что попало.

[Altenter]

Mikhail_K
Сначала у меня возникает пару Вопросов к Вам на которые Вы, может быть, мне ответите за Эйлера.

Рассмотрим эйлерову характеристику многогранника, она педставляет собой форулу включений-исключений:

Вот у нас есть один правильный многогранник, 1 многогранник со всеми своими n-гранями. Вычтем из него G граней, вместе с ними вычтутся и gG ребер, где g - количество ребер у грани. Ясное дело, что ребер вычтется больше, чем есть в многограннике, и вот ведь какая штука, количество вычтенных ребер ровно в 2 раза больше того количества ребер R, которое есть в многограннике для любого правильного многогранника. Т.е. нам надо прибавить столько же ребер, сколько есть в многограннике, чтобы мы вычли из многогранника все ребра, а не больше, чем у него есть. Ну прибавили мы эти R ребер и получилось, что мы вычли из многогранника все грани и ребра: 1- G+R.

И теперь
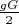
вопрос №1: G граней мы вычли с их ребрами, затем у половины граней ребра забрали $\frac{gG}{2}$ и вернули многограннику и у него стало 0 граней и 0 ребер. А грани и ребра мы вычитали и прибавляли без вершин или с вершинами? Если с вершинами, то с $R$ вычтенными ребрами мы вычли и $2R$ вершины, а вершин у нас всего V, зачем и почему тогда Эйлер вычитает из многогранника еще $V$ его вершин, если $2R$ вершин он уже и так вычел при вычитании ребер и граней???

вопрос №2: Если с вершинами, то с $R$ вычтенными ребрами мы вычли и $2R$ вершины, а вершин в многограннике у нас всего V, зачем и почему тогда Эйлер вычитает из многогранника еще $V$ его вершин, если $2R$ вершин он уже и так вычел при вычитании ребер и граней???
Т.е. тогда эйлерова характеристика имела бы вид: 1-G+R-(2R+V) и значит ребра и грани мы вычитаем и прибавляем без их вершин и тогда

вопрос №3: Почему 2 грани мы вычитаем с 1 гранями, но без 0 граней, и 1 грани мы вычитаем без 0 граней? Чтобы занулить в конце и 0-грани, вычтя тупо их и получить куб без оболочки, т.е. объем без граней, без ребер и без вершин.

Вот мы и получили многогранник без оболочки, вычтя из него оболочку: 1- многогранник с оболочкой, (G-R+V) - вычитаемая из него его поверхность и равен этот многогранник без оболочки(-1), т.е.: 1-(G-R+V)=-1, откуда G-R+V=2, что и есть эйлерова характеристика многогранника.

Собственно на вопросы адресованные к Вам я уже ответил.
Кроме вопроса о том, почему Эйлер вместо объема, 6 -ти граней кубика, 12 его ребер и 8 вершин поставил в свою характеристику 1 и все вычитал из нее. Почему???

Далее

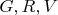
Введем обозначения: $S$- открытая единичная площадь, $L$ - открытый единичный отрезок, $G,R,V$ - грани, ребра и вершины многогранника.
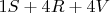
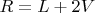
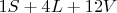
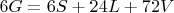
Для куба грань равна $1S+4R+4V$ , где $R=L+2V$. С учетом этого грань равна $1S+4L+12V$ 6 граней куба соответственно равны: $6G=6S+24L+72V$, пофиксили.

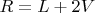
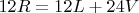
Как было показано выше, ребро многогранника равно: $R=L+2V$, а 12 ребер соответственно равно: $12R=12L+24V$, пофиксили.

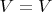
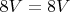
Вершина многогранника равна самой себе: $V=V$, а $8V=8V$, пофиксили.

Подставляем полученные значения для 6G, 12R, 8V в формулу для эйлеровой характеристики куба, выведенную ранее: $1-6G+12R-8V= 1-6S-24L-72V+12L+24V-8V=1-6S-12L-56V=-1$
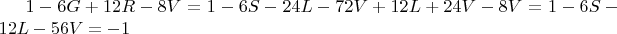
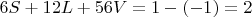
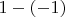
откуда: $6S+12L+56V=1-(-1)=2$ , где $1-(-1)$ - это разница между кубом в оболочке 1 и кубом без оболочки (-1). Т.е. Ваша мораль сюда не очень подходит.

[mihaild]

Altenter в сообщении #1705987 писал(а):

Вычтем из него G граней

Что это значит? Я умею вычитать числа, а вот грани вычитать из многогранника - не умею.

[Altenter]

mihaild в сообщении #1705988 писал(а):

Altenter в сообщении #1705987 писал(а):

Вычтем из него G граней

Что это значит? Я умею вычитать числа, а вот грани вычитать из многогранника - не умею.

Грань - это поверхность, являющаяся частью границы. Вы же можете отделить точку от отрезка и получить открытый отрезок? А если отделите 2 крайних точки, то получите открытый с двух сторон отрезок. А чем многогранник хуже отрезка?

[mihaild]

Altenter в сообщении #1705990 писал(а):

Вы же можете отделить точку от отрезка и получить открытый отрезок?

Что значит "отделить"?
Я, конечно, могу рассмотреть множества $[a, b]$ и $[a, b] \setminus \{b\} = [a, b)$. А зачем?
Еще я могу взять, например, куб (я тут не соглашусь с Mikhail_K, ИМХО построения лучше на конкретном примере проводить), который $[0, 1] \times [0, 1] \times [0, 1]$ и рассмотреть множество, равное разности куба (как множества) и грани, например, $\{0\} \times [0, 1] \times [0, 1]$. Получится, соответственно, множество $(0, 1] \times [0, 1] \times [0, 1]$. А вот что такое вершины, ребра и грани у этого множества - я уже не знаю.

[Altenter]

mihaild в сообщении #1705991 писал(а):

Altenter в сообщении #1705990 писал(а):

Вы же можете отделить точку от отрезка и получить открытый отрезок?

Что значит "отделить"?
Я, конечно, могу рассмотреть множества $[a, b]$ и $[a, b] \setminus \{b\} = [a, b)$. А зачем?
Еще я могу взять, например, куб (я тут не соглашусь с Mikhail_K, ИМХО построения лучше на конкретном примере проводить), который $[0, 1] \times [0, 1] \times [0, 1]$ и рассмотреть множество, равное разности куба (как множества) и грани, например, $\{0\} \times [0, 1] \times [0, 1]$. Получится, соответственно, множество $(0, 1] \times [0, 1] \times [0, 1]$. А вот что такое вершины, ребра и грани у этого множества - я уже не знаю.

А что Вы будете делать с тетраэдром, чтобы рассмотреть такую разность? И как вообще Вы определили, что это куб, не зная о его вершинах и ребрах? Я понимаю, что все хочется формализовать, но иногда ведь можно просто представить себе грани, ребра и мысленно их отделять. Ну с ребрами куба тут как раз была тема про непонятную раньше мне нотацию. где 0,1,* символы рассматривались. 000, 001,010,011,100,101,110,111 - вершины куба. 01*, 0*1, *01, 10*,1*0, *10- ребра куба, **1, *1*, 1**, **0, *0*,0**- грани куба, ***- объем куба.

[mihaild]

Altenter в сообщении #1705992 писал(а):

А что Вы будете делать с тетраэдром, чтобы рассмотреть такую разность?

Тетраэдр тоже можно задать в координатном виде, хотя и менее удобно.

Altenter в сообщении #1705992 писал(а):

И как вообще Вы определили, что это куб, не зная о его вершинах и ребрах?

Это одно из стандартных определений куба.
Но можете взять любое другое, главное - напишите его.

Altenter в сообщении #1705992 писал(а):

Я понимаю, что все хочется формализовать, но иногда ведь можно просто представить себе грани, ребра и мысленно их отделять

Ну вот я не могу. Поэтому и прошу формальные определения - они не зависят от того, кто что себе напредставлял.

[Altenter]

mihaild в сообщении #1705999 писал(а):

Это одно из стандартных определений куба.
Но можете взять любое другое, главное - напишите его.

Так написал же, в предыдущем посте, сумма всех расписанных граней и есть закрытый куб: 000, 001,010,011,100,101,110,111 - вершины куба. 01*, 0*1, *01, 10*,1*0, *10- ребра куба, **1, *1*, 1**, **0, *0*,0**- грани куба, ***- объем куба.

Вы же сами мне, если не изменяет память по этой нотации подсказывали. Вот, любую n грань можно вычесть.

[mihaild]

Altenter в сообщении #1706012 писал(а):

Так написал же, в предыдущем посте, сумма всех расписанных граней и есть закрытый куб

Что такое "расписанные грани", и что такое их сумма?

[Altenter]

mihaild в сообщении #1706015 писал(а):

Altenter в сообщении #1706012 писал(а):

Так написал же, в предыдущем посте, сумма всех расписанных граней и есть закрытый куб

Что такое "расписанные грани", и что такое их сумма?

Хорошо, перечислены грани. Их сумма- закрытый куб.

[mihaild]

Altenter в сообщении #1706016 писал(а):

Их сумма

mihaild в сообщении #1706015 писал(а):

что такое их сумма?

-- 15.10.2025, 20:23 --

На всякий случай поясню: чтобы говорить о сумме каких-то объектов, на них нужно определить сложение.
Еще неплохо бы определить сами объекты. Строки в алфавите $\{0, 1, *\}$? А для тетраэдра или додекаэдра?

[Altenter]

mihaild в сообщении #1706019 писал(а):

Altenter в сообщении #1706016 писал(а):

Их сумма

mihaild в сообщении #1706015 писал(а):

что такое их сумма?

Объединение куба и его границы, которая разбита на части- n-грани.

-- 15.10.2025, 21:33 --

Еще в топологии есть слово "сшивание", но я не специалист в математике и не могу судить, насколько оно здесь уместно в этом смысле.