Найдем приближенное решение уравнения Вольтерра и убедимся, что при различных значениях

возможны и затухающие колебания и монотонно убывающие решения.
Чтобы получить приближенное решение, ограничимся в выражении для
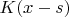
первым слагаемым в сумме т.е.:
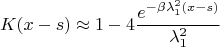
Продифференцируем исходное уравнение:
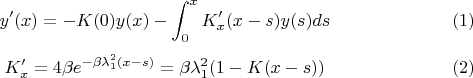
Подставим

в

и, используя исходное уравнение, получим:
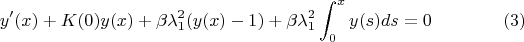
Дифференцируем

и получаем ДУ:
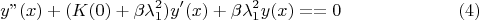
Решаем соответствующее характеристическое уравнение и находим показатели экспонент:
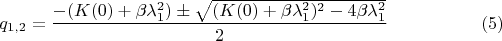
Из

видно, что в зависимости от величины параметра

возможны как затухающие колебания, так и монотонное убывание.