Ферма утверждал, что уравнение

не имеет решений в рациональных числах.
Попробуем доказать обратное.
Предположим, что такое решение существует
при

,

,

, где

,

,

- целые положительные взаимно простые числа и

, то есть

.
1.1.

, где

- целое положительное число

, где

- целое положительное число.
1.2.

,

Перемножаем левые и правые части, получаем:

,

1.3.

,

(п.1.1). Перемножаем левые и правые части, получаем:

, следовательно,

.
2.1.1 функция
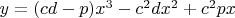
в точках

и

принимает одинаковые значения разных знаков и она является целой рациональной функцией, непрерывна и определена при всех значениях

, следовательно, между

и

существует точка ( назовем ее

, значение функции в которой равно

.
2.1.3 Найдем все точки, значение функции в которых равно нулю.

.

или


, отсюда

или

.
Поскольку

,

,

-рациональное число.
3.1.поскольку
функция

является целой рациональной функцией, непрерывна и определена при всех значениях

и ее значение равно нулю в точках 0, h и с,
существует три точки, в которых она принимает одинаковые отрицательные значения (

,

и

) и три , в которых она принимает одинаковые положительные значения (

,

и

).
Эти числа действительные (поскольку если бы они были комплексными, это противоречило бы существованию рационального

между

и

)
3.2 Пусть
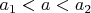
3.3

(сумма корней уравнения по Теореме Виета), при этом

- рациональное число,

- рациональное число.
4.1
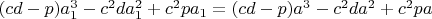

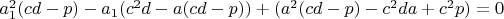
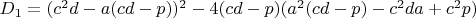

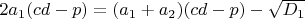
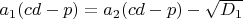
4.2
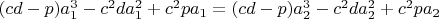
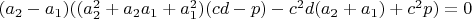
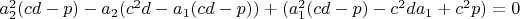
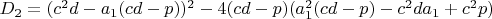
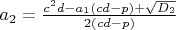
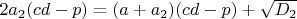
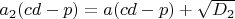
5.1
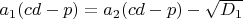
(п 4.1)
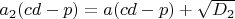
(п 4.2)

- рациональное число (п.3.3)
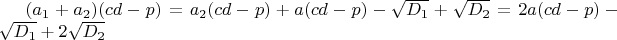
следовательно,
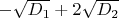
- рациональное число.
Поскольку

- целое число, чтобы выполнялось равенство,

должно быть рaциональным числом.
5.2 То есть,
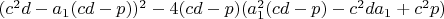
-рациональное число,
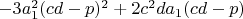
- рациональное число,
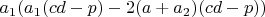
-рациональное число,
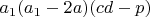
-рациональное число,
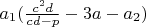
-рациональное число,
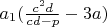
-рациональное число, следовательно,

-рациональное число,

-рациональное число.
Аналогично доказывается рациональность

и

.
6.1 Пусть

,

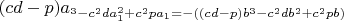
(п.1.3)
Тогда
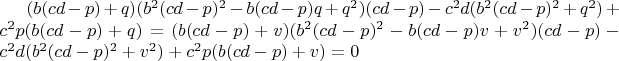
,
следовательно,
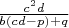
-целое число,
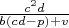
-целое число.
6.2
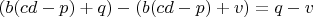
Но
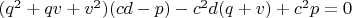
, следовательно,

- целое число.

, следовательно, у
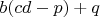
и
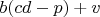
может быть только один общий с

делитель ( кроме

и

) - это

, если

делится на

.
Но поскольку

, либо
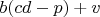
, либо,
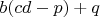
должны иметь общий делитель с

помимо

,

и

.
6.3 Пусть
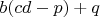
имеет общий делитель с

.
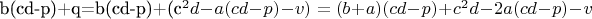
. Следовательно,
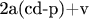
имеет общий делитель с

.
6.4
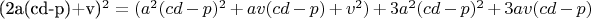
, следовательно,
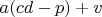
имеет общий делитель с
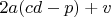
и

. Следовательно,

имеет общий делитель с
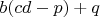
и

,

имеет общий делитель с
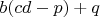
и

,
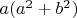
имеет общий делитель с
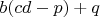
и

,
но это невозможно, поскольку

и

-взаимно простые числа,
a

не делится на

.
Мы пришли к противоречию. Значит, наше первоначальное предположение о том, что уравнение

имеет решение в целых числах, было неверным.
Уравнение

не имеет решений в целых числах.
Если эта цепочка рассуждений верна, точно так же доказывается невозможность для всех нечетных степеней >2.