Задача: доказать, что
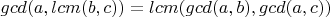
. gcd - наибольший общий делитель, lcm - наименьшее общее кратное.
Если обозначить
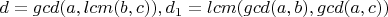
, то у меня получилось доказать, что
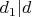
(

делит

). Теперь, нужно бы, по идее, доказать обратное, но что-то не выходит. Например, можно сказать, что
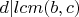
, а значит делит также и

и

, где
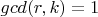
. Но отсюда не следует, что

делит по отдельности

и

, что пригодилось бы для дальнейшего доказательства.
-- 01.10.2025, 07:42 --Да, и желательно доказать без основной теоремы арифметики.