Кажется, что здесь всё не так просто. Если обсуждаемая система имеет нетривиальные решения, то график параметрически заданной функции
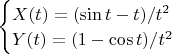
должен иметь самопересечения или касания. Я их не обнаружил.
Да, действительно не всё так просто. В том примере, что я привёл из отрезка
![$[-6.4\cdots -6],~~x_0$ $[-6.4\cdots -6],~~x_0$](https://dxdy-04.korotkov.co.uk/f/7/e/e/7ee6c13a3371c6519180fdbc96199e2182.png)
численно совпал с

с точностью до всех доступных мне знаков:
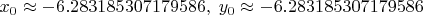
Но вот уже для следующего корня из отрезка
![$[-9.1\cdots-8.9]$ $[-9.1\cdots-8.9]$](https://dxdy-02.korotkov.co.uk/f/1/a/f/1afbc882c8c9e7245b711a1a12b6e61582.png)
значения

и

различаются в пятом знаке после запятой:
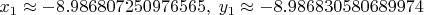
(в то время, как уравнение

имеет корень
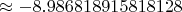
на этом отрезке)
Т.е. похоже на то, что нетривиальные решения расположены очень близко к тривиальным. Если у кого есть возможность проверить это с большой точностью, было бы неплохо.