Корректно ли такаое суммирование ряда Гранди?

[Altenter]

Интересно, насколько корректен и приемлем с математической точки зрения такой способ суммирования ряда Гранди:
Рассмотрим бесконечный и безначальный знакочередующийся ряд:

$............-1+1-1+1-1+1-1+1-1+1-1+1-............... $
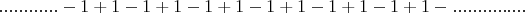
Если положить, что 1 - это смещение идеального маятника из левой крайней точки в правую, а -1, наоборот из правой крайней точки в левую, то данный ряд будет выражать физическую модель маятника, который безначально вечно совершал свободные колебания в прошлом и будет вечно колебаться в будущем. С физической точки зрения это значит, что данный маятник никогда ни с чем не взаимодействовал и не будет взаимодействовать, поэтому его невозможно обнаружить и, можно сказать, что его не существует. Математически, несуществование маятника выражается в приравнивании исходного ряда нулю:

$............-1+1-1+1-1+1-1+1-1+1-1+1-...............=0$
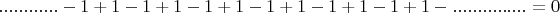
Теперь мысленно вычленим в произвольном месте этого ряда -1:

$............-1+1-1+1-1+1(-1)+1-1+1-1+1-...............=0$

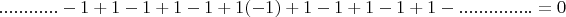
и перенесем её в правую часть, вычтя из обеих сторон равенства:

$............-1+1-1+1-1+1+1-1+1-1+1-...............=1$

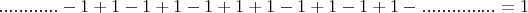
Мысленно разобьем левую часть равенства в том месте где стояла -1:

$............-1+1-1+1-1+1|+1-1+1-1+1-1+...............$
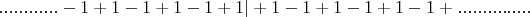
Теперь обратим внимание на то, что получили 2 одинаковые по составу части, каждая из которых является зеркальным отображением другой и которые в сумме дают 1. Бессмысленно говорить о том, что стоит в "конце" каждой части, поскольку каждая из них бесконечна и не имеет этого самого конца. Поэтому, просто приравняем эти части друг другу, поскольку они начинаются одинаково и одинаково не заканчиваются.
Т.к. их сумма равна 1, а сами части тождественны друг другу, если суммирование каждой из них проводить от места разделения, то очевидно, что каждая из частей равна 0.5:

$............-1+1-1+1-1+1=+1-1+1-1+1-...............=0.5 $
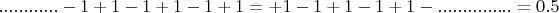
При этом каждая из представленных частей тождественна ряду Гранди, а результат суммирования эквивалентен результату суммированию по Чезаро, при выводе мы не выходили за рамки простых арифметических операций. Вот интересно, если на основе физических рассуждений о маятнике можно решить математическую задачу, то почему нельзя на основе физики доказать гипотезу Римана, как это попыталься сделать М.Атья? В чем недостаток и нематематичность этого подхода?

[mihaild]

Altenter в сообщении #1703309 писал(а):

ряда Гранди:
Рассмотрим бесконечный и безначальный знакочередующийся ряд

Так ряд Гранди или безначальный? У ряда Гранди есть начало.

Altenter в сообщении #1703309 писал(а):

Если положить, что 1 - это смещение идеального маятника из левой крайней точки в правую

То никакого отношения к математике всё дальнейшее иметь не будет.

[Altenter]

mihaild в сообщении #1703312 писал(а):

Так ряд Гранди или безначальный? У ряда Гранди есть начало.

Безначальный ряд разбивается на 2 ряда Гранди, после вычленения (-1) и переноса ее в правую сторону, но вы до этого не дочитали т.к.

mihaild в сообщении #1703312 писал(а):

никакого отношения к математике всё дальнейшее иметь не будет.

Спасибо.
И тогда вопрос: можно ли этот безначально-бесконечный ряд как-то просто приравнять к 0 не прибегая к физическим соображениям?

[serg_yy]

Без определения того, что понимается в данном случае под суммой ряда, всё это является философией. В обычном смысле данный ряд, разумеется, расходится, то есть вообще не имеет суммы.

[mihaild]

Altenter в сообщении #1703315 писал(а):

И тогда вопрос: можно ли этот безначально-бесконечный ряд как-то просто приравнять к 0 не прибегая к физическим соображениям?

С формальной точки зрения, происходит следующее.
У нас есть множество бесконечных (в две стороны) последовательностей. И мы хотим на каком-то его подмножестве определить функционал, который будем называть "суммой ряда" так, чтобы были выполнены какие-то свойства. И дальше вопрос, какие именно.

[Altenter]

serg_yy в сообщении #1703317 писал(а):

Без определения того, что понимается в данном случае под суммой ряда, всё это является философией. В обычном смысле данный ряд, разумеется, расходится, то есть вообще не имеет суммы.

Да, согласен с Вами, но давно уже задумываюсь о необходимости введения в теорию рядов понятия неоднозначной сходимости, вот на примере этого как раз ряда Гранди можно увидеть, что конечная его сумма всегда либо 0, либо 1 и конечные суммы присутствуют одинаково, т.е. чередуются. Значит его сходимость на бесконечности двузначная: [0,1], а среднее между этими двумя значениями и есть 0.5, которое получил Чезаро.

-- 26.09.2025, 16:49 --

mihaild в сообщении #1703318 писал(а):

У нас есть множество бесконечных (в две стороны) последовательностей. И мы хотим на каком-то его подмножестве определить функционал, который будем называть "суммой ряда" так, чтобы были выполнены какие-то свойства. И дальше вопрос, какие именно.

Не суммируемые ряды могут быть суммируемыми многозначно, как было сказано выше, а если они суммируются многозначно, то их средняя сумма - есть среднее их сумм с учетом пропорции их присутствия. Вот оно и будет суммой такого не сходящегося в обычном смысле ряда.

[mihaild]

Altenter в сообщении #1703319 писал(а):

Не суммируемые ряды могут быть суммируемыми многозначно, как было сказано выше, а если они суммируются многозначно, то их средняя сумма - есть среднее их сумм с учетом пропорции их присутствия.

Это подходит под моё описание. Никакой "многозначной суммы" тут не нужно. А нужны строгие определения, какие хочется иметь свойства у этого функционала.

[Altenter]

mihaild в сообщении #1703329 писал(а):

Altenter в сообщении #1703319 писал(а):

Не суммируемые ряды могут быть суммируемыми многозначно, как было сказано выше, а если они суммируются многозначно, то их средняя сумма - есть среднее их сумм с учетом пропорции их присутствия.

Это подходит под моё описание. Никакой "многозначной суммы" тут не нужно. А нужны строгие определения, какие хочется иметь свойства у этого функционала.

Ну какие свойства, хочется, чтобы сумма как-то отражала реальные процессы, как тот же идеальный маятник, как-то с ними соотносилась, как какое-то среднее значение или еще как-то. Математика создается ведь для применения в описании реальности. Т.е. там где нельзя выразить числом какую - то величину придумали среднее значение. Было бы неплохо чтобы это среднее было вещественным числом. То же самое и у какого-то класса несуммируемых рядов, хотелось бы чтобы их сумма выражалась числом, также как и сумма сходящихся рядов. Если честно, я не понимаю о каком функционале Вы говорите.

[Red_Herring]

Имеются разнообразные неэквивалентные способы суммирования расходящихся рядов. Приложите хотя бы минимальные усилия сами––спросите у ИИ.

[ozheredov]

Altenter в сообщении #1703309 писал(а):

почему нельзя на основе физики доказать гипотезу Римана

Я так теорему Ферма доказал. Пусть $a$ - размер рептилоида $A$. Тогда $a^n$ - объем его личного многомерного пространства. Аналогично, $b^n$ и $c^n$. Тогда равенство $a^n + b^n = c^n$ означает, что $A$ и $B$ влезли в личное пространство рептилоида $C$, что противоречит первому закону универсальной интроверсии. Теорема доказана.