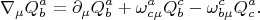Спиновая динамика на геодезических

[Theoristos]

Предположим, у нас есть источник, излучающий луч света с круговой поляризацией, так что каждый фотон в луче имеет поляризацию +1.

Далее, пусть мы пускаем его мимо чёрной дыры, которая поворачивает этот луч... скажем, на 90 градусов.

Вопрос - какова будет поляризация фотонов в луче после поворота?


* Ну, и, как расширение, другие частицы, массивные, фермионы - какая у них получается динамика спина при свободном движении в грав. поле?
Где-то этот вопрос рассматривается?

[Утундрий]

Вообще-то здесь хорошо бы порешить искривлённого Максвелла, но если спин — просто так спин, то в "ОТО" И. Б. Хрипловича этим делам посвящена вся седьмая глава.

[Theoristos]

Утундрий в сообщении #1703146 писал(а):

Вообще-то здесь хорошо бы порешить искривлённого Максвелла

Тоже думал над этим, но показалось, что спин - вернее и квантомеханичнее

Утундрий в сообщении #1703146 писал(а):

в "ОТО" И. Б. Хрипловича этим делам посвящена вся седьмая глава.

А применительно к такому вопросу каков там вердикт?

Глянул - как-то тяжеловато и совершенно не квантомеханически.

[Утундрий]

Theoristos в сообщении #1703155 писал(а):

как-то тяжеловато и совершенно не квантомеханически.

Так где ОТО, а где КМ?

Вопрос отметил, потом подумаю, но сейчас у меня мысли в другом направлении скачут.

[SergeyGubanov]

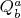
Действие для пробной частицы массы $m$ обладающей относительно локальной тетрады $e^{\mu}_{a}$ спиновым "зарядом" $Q^{a}_{b}$ я записал бы так:

$$ S = \int \left( - m \, \sqrt{ g_{\mu \nu} dx^{\mu} dx^{\nu} } + Q^{a}_{b} \omega^{b}_{a \mu} dx^{\mu} \right). $$

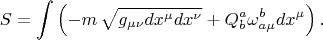
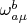
Здесь $\omega^{b}_{a \mu}$ - спиновая (тетрадная) связность, это та которая определяет ковариантную производную от тетрады:

$$ \nabla_{\mu} e^{\nu}_a = \partial_{\mu} e^{\nu}_a + \Gamma^{\nu}_{\rho \mu} e^{\rho}_{a} - \omega^{b}_{a \mu} e^{\nu}_{b}. $$

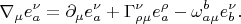
Ещё будет полезным уравнение ковариантного постоянства этого самого спинового "заряда" $\nabla_{\mu} Q^{a}_{b} = 0$.

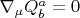
На всякий случай, напишу в явном виде:

$$ \nabla_{\mu} Q^{a}_{b} = \partial_{\mu} Q^{a}_{b} + \omega^{a}_{c \mu} Q^{c}_{b} - \omega^{c}_{b \mu} Q^{a}_{c}. $$

[SergeyGubanov]

(Про седьмую главу ОТО Хрипловича)

Посмотрел седьмую главу ОТО Хрипловича. Он начинает с трёхмерного вектора спина, а потом обобщает его до четырёхвектора спина. Для четырёхвектора спина записывает уравнение его динамики в ОТО. Я не осуждаю конечно, просто испытываю затруднение понять, а что так можно было? Не бывает никакого четырёхвектора спина. О трёхмерном векторе спина можно говорить только лишь потому, что трёхмерная 2-форма дуальна трёхмерной 1-форме. Другими словами, в трёхмерии можно ввести трёхмерный вектор дуальный антисимметричному тензору второго ранга: $s_{k} = s^{i j} \varepsilon_{i j k}$. А в четырёхмерии, в пятимерии и так далее никакого "вектора спина" нет и быть не может. Есть 2-форма спина.

[Theoristos]

В процессе поисков навикипедились некие "Mathisson–Papapetrou–Dixon equations", "уравнения движения классического вращающегося тела".

[url]http://en.wikipedia.org/wiki/Mathisson–Papapetrou–Dixon_equations[/url]


[url=http://en.wikipedia.org/wiki/Mathisson–Papapetrou–Dixon_equations]https://en.wikipedia.org/wiki/Mathisson–Papapetrou–Dixon_equations[/url]


ps: хм, а тег [url][/url] на форуме сломался?

[Утундрий]

Theoristos в сообщении #1703271 писал(а):

[url]http://en.wikipedia.org/wiki/Mathisson–Papapetrou–Dixon_equations[/url]

Mathisson Papapetrou Dixon equations

[SergeyGubanov]

https://en.wikipedia.org/wiki/Mathisson%E2%80%93Papapetrou%E2%80%93Dixon_equations писал(а):

$$ k_\nu= \int_{t=\operatorname{const}} {T^0}_\nu \sqrt{g} d^3 x $$

https://en.wikipedia.org/wiki/Mathisson%E2%80%93Papapetrou%E2%80%93Dixon_equations писал(а):

$$ S^{\mu\nu} = \int_{t=\operatorname{const}}\left\{\left(x^\mu - X^\mu\right)T^{0\nu} - \left(x^\nu - X^\nu\right)T^{0\mu}\right\} \sqrt{g}d^3 x $$

Там же интегралы берут от компонент тензора...

(Оффтоп)

Брать интегралы от компонент тензора примерно так же разумно как четырёхвектор спина умножать на четырёхвектор магнитного поля.

[SergeyGubanov]

SergeyGubanov в сообщении #1703170 писал(а):

Ещё будет полезным уравнение ковариантного постоянства этого самого спинового "заряда" $\nabla_{\mu} Q^{a}_{b} = 0$.

Это почти 100% не правильно. Как правильно не знаю.

Похожую тему можно обсудить там: topic161725.html