сколько мучений из-за этих псевдовекторных обозначений.
Неча на наблу пенять коли ручки кривые ...

Я сейчас поясню как надо обращаться с наблой.
1. Давайте посчитаем
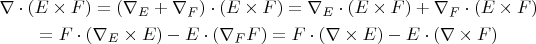
в первой строчке мы заменяем общую наблу на сумму двух, одна из которых применяется к

, а вторая к

(это из-за правила Лейбница), потом применяем обычные формулы для смешанного произведения, утаскивая тот сомножитель на который "конкретная" набла не действует, налево. А затем опускаем ставший ненужным индекс.
2. Попробуйте сами посчитать этим методом
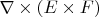
, используя "бац минус цаб" правило двойного векторного умножения :
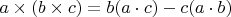
плюс то же правило Лейбница. Везде все сомножители векторные