Запись векторной операции

[sergey zhukov]

В одном месте увидел, что в записи уравнения Навье-Стокса используется такое выражение:

$$\nabla.(\vec{u}\vec{u})$$

Там оно, очевидно, должно соответствовать вот этому:

$$\vec{u}(\nabla \cdot\vec{u})$$

Не совсем понятна логика скобок. Вроде бы нужно сначала действие в скобках выполнять. Но поскольку в скобках написана какая-то непонятная операция над двумя векторами, то нужно сначала скалярно умножить первый вектор скорости на наблу, а потом на полученный скаляр умножить на второй вектор скорости? Или как эту запись понимать?

[EUgeneUS]

sergey zhukov
Не знаю, какое отношение это имеет к уравнению Навье-Стокса. Но обе записи корректные и читаются так:

1. $\nabla (\vec{u}\vec{u})$

Умножить вектор $\vec{u}$ скалярно на самого себя, после чего применить оператор набла. Так как скалярный квадрат вектора - скаляр, то оператор набла тут будет означать градиент.

2. $\vec{u}(\nabla \cdot\vec{u})$

Применить оператор набла к вектору $\vec{u}$ (то есть это дивергенция $\vec{u}$), после чего скалярно умножить на сам вектор $\vec{u}$.

Известно тождество: $\nabla(\vec{v}\vec{u}) = \vec{v} \nabla \vec{u} + \vec{u} \nabla \vec{v}$

Откуда $\nabla (\vec{u}\vec{u}) = 2 \vec{u}(\nabla \cdot\vec{u})$

-- 21.09.2025, 20:08 --

К вопросу об уравнении Навье-Стокса.

Обе этих записей ни в коем случае нельзя путать с записью:

$$(\mathbf{v} \cdot \nabla)\mathbf{v}$$

которая читается так:
1. Сформировать дифференциальный оператор

$$(\mathbf{v} \cdot \nabla) = v_i \frac{\partial}{\partial x_i} = v_1 \frac{\partial}{\partial x_1} + v_2 \frac{\partial}{\partial x_2} + v_3 \frac{\partial}{\partial x_3}$$

2. А потом применить его к вектору $\mathbf{v}$

С учетом правила суммирования по повторяющимся индексам:

$$((\mathbf{v} \cdot \nabla)\mathbf{v})_i \equiv v_k \frac{\partial v_i}{\partial x_k} $$

[Red_Herring]

Я подореваю, что под $\vec{u}\vec{u} $ понимается тензор $u_iu_j$, и тогда под $\nabla(\vec{u}\vec{u}) $ понимается $\partial_i(u_iu_j)= (\vec{u}\cdot \nabla) \vec{u} + (\nabla \cdot \vec{u})\vec{u}$. Однако я не ясновидящий и не знаю что автор имел в виду, но знаю что такие вещи приличные авторы объясняют.

[sergey zhukov]

EUgeneUS

$$\nabla (\vec{u} \cdot \vec{u})=(\frac{\partial (u_x^2+u_y^2+u_z^2)}{\partial x}, \frac{\partial (u_x^2+u_y^2+u_z^2)}{\partial y}, \frac{\partial (u_x^2+u_y^2+u_z^2)}{\partial z})$$

Это выражение - совсем не то, что нужно. Там точно не это имелось ввиду. Там после наблы точка стоит. Я думаю, это значит, что на наблу нужно скалярно умножать.

$$\vec{u}(\nabla \cdot \vec{u})=\vec{u}(\frac{\partial u_x}{\partial x}+\frac{\partial u_y}{\partial y}+\frac{\partial u_z}{\partial z})=(u_x(\frac{\partial u_x}{\partial x}+\frac{\partial u_y}{\partial y}+\frac{\partial u_z}{\partial z}), u_y(\frac{\partial u_x}{\partial x}+\frac{\partial u_y}{\partial y}+\frac{\partial u_z}{\partial z}),u_z(\frac{\partial u_x}{\partial x}+\frac{\partial u_y}{\partial y}+\frac{\partial u_z}{\partial z}))$$

Это, да, тоже не то.

А эти выражения, как я вначале думал, одно и то же:

$$(\vec{u}\cdot \nabla)\vec{u}=\vec{u}(\nabla \cdot \vec{u})$$

Но вот как раз нет:

$$(\vec{u}\cdot \nabla)\vec{u}=(u_x\frac{\partial u_x}{\partial x}, u_y\frac{\partial u_y}{\partial y}, u_z\frac{\partial u_z}{\partial z})$$

-- 21.09.2025, 21:51 --

Red_Herring
Например, стационарное уравнение Навье-Стокса там было записано так:

$$\nabla.(\vec{u}\vec{u})=-\frac{1}{\rho}\nabla p+\nabla.(\nu\nabla \vec{u})$$

[Red_Herring]

sergey zhukov в сообщении #1702667 писал(а):

Например, стационарное уравнение Навье-Стокса там было записано так:

Т.е. так, как я расписал левую часть (с учетом нулевой дивергенции)

[sergey zhukov]

sergey zhukov в сообщении #1702667 писал(а):

Но вот как раз нет:

$$(\vec{u}\cdot \nabla)\vec{u}=(u_x\frac{\partial u_x}{\partial x}, u_y\frac{\partial u_y}{\partial y}, u_z\frac{\partial u_z}{\partial z})$$

Опять я тут напутал. На самом деле должно быть:

$$(\vec{u}\cdot \nabla)\vec{u}=(v_x\frac{\partial v_x}{\partial x}+v_y\frac{\partial v_x}{\partial y}+v_z\frac{\partial v_x}{\partial z}, v_x\frac{\partial v_y}{\partial x}+v_y\frac{\partial v_y}{\partial y}+v_z\frac{\partial v_y}{\partial z}, v_x\frac{\partial v_z}{\partial x}+v_y\frac{\partial v_z}{\partial y}+v_z\frac{\partial v_z}{\partial z})$$

[Утундрий]

sergey zhukov в сообщении #1702592 писал(а):

оно, очевидно, должно соответствовать вот этому:

Вообще ни разу не очевидно. Первое — дивергенция диадика, а второе есть производная по направлению от вектора. Равны друг другу они только в силу уравнения неразрывности, кое в случае НС означает просто бездивергентность поля скорости.

[EUgeneUS]

sergey zhukov в сообщении #1702667 писал(а):

А эти выражения, как я вначале думал, одно и то же:

$$(\vec{u}\cdot \nabla)\vec{u}=\vec{u}(\nabla \cdot \vec{u})$$

Это, кстати, грубая, но распространенная ошибка.
Набла хоть и похожа чем-то на вектор, вектором не является.
И нужно помнить, что
а) что стоит справа от наблы - на то набла действует.
б) что стоит слева от наблы - на то набла просто умножается.

Если справа от наблы ничего не стоит, то это не вектор и не скаляр, а дифференциальный оператор.
Иногда говорят "набла не коммутирует с векторами". Так она и со скалярами не коммутирует. $\nabla f$ и $f \nabla$ - две большие разницы.

[sergey zhukov]

EUgeneUS
Ну да. Сбивает с толку знак умножения в $\nabla \cdot \vec{u}$. Если уж просто действует, так напиши $\nabla \vec{u}$. Видимо, в промежуточных выкладках так удобнее считать наблу за вектор.

[Утундрий]

sergey zhukov в сообщении #1702907 писал(а):

Сбивает с толку знак умножения в $\nabla \cdot \vec{u}$. Если уж просто действует, так напиши $\nabla \vec{u}$. Видимо, в промежуточных выкладках так удобнее считать наблу за вектор.

Он там не просто так стоит, а обозначает свёртку.

[EUgeneUS]

Утундрий в сообщении #1702912 писал(а):

Он там не просто так стоит, а обозначает свёртку.

Разъясните, пожалуйста, чем в этом случае свертка (суммирование по повторяющемуся индексу, насколько понимаю), отличается от формального применения скалярного произведения (что тоже выражается в суммирование по повторяющемуся индексу).
Понятно, что если слева стоит набла, то это не есть скалярное произведение, как таковое. А есть применение дифференциального оператора.

[Red_Herring]

sergey zhukov в сообщении #1702907 писал(а):

Видимо, в промежуточных выкладках так удобнее считать наблу за вектор.

Набла и есть вектор, а также дифференциальный оператор строго первого порядка. Поэтому надо применять правила векторной алгебры, где есть два умножения векторов, и правило Лейбница. А вот что такое когда знака умножения нет? Это будет порождение тензора 2го ранга.

EUgeneUS в сообщении #1702993 писал(а):

Разъясните, пожалуйста, чем в этом случае свертка (суммирование по повторяющемуся индексу, насколько понимаю), отличается от формального применения скалярного произведения (что тоже выражается в суммирование по повторяющемуся индексу).

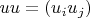
Если справа от наблы стоит вектор, то индекс только один и будет скалярное произведение. А вот если индексов больше, как в $uu = (u_iu_j)$, какой тогда индекс повторяется? Поэтому и говорят "свертка" и указывают по каким индексам. Да, в нашем специальном случае тензор симметричен, и поэтому неважно, но правила придумывают для общего случая.

[Утундрий]

EUgeneUS
Набла могла бы и просто стоять. Для краткости так обозначают тензорное произведение. Точка же указывает на то, что нужно скалярно умножить наблу на соседний с ней (через точку) вектор.

[Geen]

Ёлки, сколько мучений из-за этих псевдовекторных обозначений...

[Утундрий]

И действительно. Дам универсальный совет: пишите всё в компонентах. Тогда точно не ошибётесь.