Нам надо найти все целые

, для которых
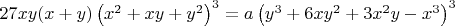
В общем, да. В конечном итоге все сведется именно к этому. Здесь придется решать уравнения Туэ, что, конечно, неэлементарно, но мы будем считать, что системы компьютерной алгебры умеют их корректно решать. В итоге мы получим только два значения

--- ровно те, что приведены выше. (Кстати, не обязательно предполагать, что

имеет вид
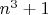
. Можно из исходного уравнения выразить

через

и

, а затем, пользуясь однородностью, считать

и

взаимно простыми.)
Но это только половина дела: как я уже писал выше, используемая упрощающая формула получена при дополнительных ограничениях. Нужно еще показать, что общий случай сводится к этому (вдруг есть упрощающие формулы другого типа?). Оказывается, здесь тоже интересно и тоже неэлементарно.
В целом, задача как олимпиадная --- так себе задача (требует слишком много специальных знаний). Но ответ забавный.