Что-то запутался в простой вещи. Рассмотрим единичную сферу, на ней точку

. В точке - внешнюю нормаль и касательную плоскость, которая ей перпендикулярна.
Касательные вектора

лежат в этой плоскости. Поскольку центр сферы в начале координат, для координат (единичного) касательного вектора получаем систему:
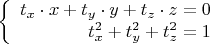
То есть одна координата - это свободный параметр. Но я бы хотел другую параметризацию.
А именно - будем "смотреть" вдоль нормали. Тогда положение касательного вектора также задается одним параметром - неким углом вращения в касательной плоскости. Но от чего отсчитывается этот угол? Как потом все обратно пересчитать в декартовы координаты?