Упрощаемый двойной радикал

[nnosipov]

Для каких целых чисел $a$, не являющихся точными кубами, двойной радикал

$$\sqrt[3]{1+\sqrt[3]{a}}$$

можно записать как сумму обычных радикалов над полем рациональных чисел? (Значения всех радикалов предполагаются вещественными.)

[Утундрий]

nnosipov в сообщении #1702506 писал(а):

обычных радикалов

Это, простите, что за звери?

[nnosipov]

Утундрий в сообщении #1702512 писал(а):

Это, простите, что за звери?

Да это просто корни какой-то степени из рациональных чисел --- типа $\sqrt[4]{7}$, $\sqrt[3]{-4/5}$ и т.п. Формальное определение таково: число $\omega \in \mathbb{R}$ называется (вещественным) радикалом степени $n>1$ над полем $\mathbb{Q}$, если $\omega^k \not\in \mathbb{Q}$ при $1 \leqslant k<n$, а $\omega^n \in \mathbb{Q}$.

[Утундрий]

А, понятно, спасибо. Помнится, на лекциях ТФКП различали т.н. арифметические корни (в рамках темы "обычные") и т.н. "комплексные", которые при возведении в соответствующую степень дают ровно подкоренное выражение (и которых, таким образом, имеется несколько штук). Кстати, у меня до сих пор имеется привычка отмечать "комплексные корни" на письме двойной косой полкой радикала. В ТеХе же я такой возможности пока не нашёл.

[nnosipov]

Чтобы заинтриговать: такие целые числа $a$ существуют, например $a=-2$:

$$\sqrt[3]{1-\sqrt[3]{2}}=-\sqrt[3]{\frac{1}{9}}+\sqrt[3]{\frac{2}{9}}-\sqrt[3]{\frac{4}{9}}$$

(хорошо известный пример Рамануджана). Есть ли еще?

[Dendr]

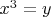
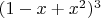
А интересно выходит. Обратным ходом можно прийти к этой форме так: рассмотрим неизвестное $x$, такое, что $x^3=y$ - рациональное, и разложим $(1-x+x^2) ^3$ по "степеням" $x$:

$$(y^2-7y+1)+(6y-3) x+(6-3y) x^2$$

.

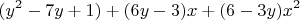
Один член лишний, его следует занулить. Положив $y=2$ и "поиграв" коэффициентами, получим пример Рамануджана. Для 0.5 - тоже. "Свободный" так не дастся без вложенных радикалов, так что нового решения не даст.

Попытался обобщить трехчлен, с которого начал, и все свелось к дроби, где в числителе полином 8 порядка, в знаменателе 9. При единице в аргументе (как раз случай нашего индийского друга) он равен 2, а дальше - убывает. Так что видимо нет.
Но это абсолютно кривое доказательство (вообще ее доказательство), даже стыдно целиком его приводить. Да и рассматривает оно ровно одну конфигурацию радикалов.

Только на голой интуиции понятно, что только она и работает: там собственно кубический корень из $a$, его же квадрат и единица образуют линейную комбинацию с некими рациональными коэффициентами и (возможно) общим радикальным множителем, после возведения в куб перейдет в другую линейную комбинацию из же, но теперь радикал в общем множителе исчезнет. То есть такая специфическая алгебра, в которой возникли "а ля" диофантовы уравнения.

[nnosipov]

Dendr
Спасибо, это оригинально, но, кажется, интрига сохраняется. Вот, скажем, deepseek после глубоких раздумий (более 20 минут) считает, что такие значения $a$ существуют, причем в товарном количестве, и сообщает наименьшее из них --- $a=7$. Интересно, можно ли его допытать до истинной правды? Тоже интрига.

[Rak so dna]

тут:

$\sqrt[3]{3\sqrt[3]{xy(x+y)}-\left(y^3+6xy^2-3x^2y-x^3\right)}=\sqrt[3]{x^2y}-\sqrt[3]{y^2(x+y)}+\sqrt[3]{x(x+y)^2}$

[nnosipov]

Rak so dna
Насколько я понял, в этой статье авторы рассматривают задачу упрощения двойного радикала не во всей общности: априори предполагается, что упрощающее выражение содержит только кубические радикалы над $\mathbb{Q}$ (см. предложение 1). У нас же никаких ограничений на степень радикалов в упрощаемом выражении нет.

Да, а ответ-то какой?

[nnosipov]

Rak so dna в сообщении #1702683 писал(а):

тут:

$\sqrt[3]{3\sqrt[3]{xy(x+y)}-\left(y^3+6xy^2-3x^2y-x^3\right)}=\sqrt[3]{x^2y}-\sqrt[3]{y^2(x+y)}+\sqrt[3]{x(x+y)^2}$

По-моему, здесь опечатка (подставьте $x=y=1$). И, похоже, в оригинальной статье Зиппеля тоже, но уже другая. Я эту статью Зиппеля смотрел много раз, а опечатку заметил только сейчас.

Upd. В общем, Зиппель (см. Zippel R. Simplification of expressions involving radicals // J. of Symbolic Computation. 1985. Vol. 1. P. 189-210) допустил опечатку (забыл квадратичный сомножитель перед внутренним радикалом слева), а авторы из СПб добавили еще свою собственную опечатку --- написали $-3x^2y$ вместо правильного $+3x^2y$). Короче, вот правильный вариант:

$\sqrt[3]{3(x^2+xy+y^2)\sqrt[3]{xy(x+y)}-\left(y^3+6xy^2+3x^2y-x^3\right)}=$

$=\sqrt[3]{x^2y}-\sqrt[3]{y^2(x+y)}+\sqrt[3]{x(x+y)^2}$

[Rak so dna]

nnosipov да, действительно (меня сразу смутило нарушение однородности)

Вроде так работает:

$$\sqrt[3]{3(x^2+xy+y^2)\sqrt[3]{xy(x+y)}-\left(y^3+6xy^2+3x^2y-x^3\right)}=\sqrt[3]{x^2y}-\sqrt[3]{y^2(x+y)}+\sqrt[3]{x(x+y)^2}$$

[nnosipov]

Rak so dna в сообщении #1702713 писал(а):

меня сразу смутило нарушение однородности

А я только сейчас обратил на это внимание

Rak so dna в сообщении #1702713 писал(а):

Вроде так работает:

$$\sqrt[3]{3(x^2+xy+y^2)\sqrt[3]{xy(x+y)}-\left(y^3+6xy^2-3x^2y-x^3\right)}=\sqrt[3]{x^2y}-\sqrt[3]{y^2(x+y)}+\sqrt[3]{x(x+y)^2}$$

Все-таки слева должно быть $+3x^2y$. Проверьте еще раз.

Итого, в двух научных статьях есть вопиющие опечатки, но ни авторы, ни читатели их не видят

[Rak so dna]

nnosipov в сообщении #1702715 писал(а):

Все-таки слева должно быть $+3x^2y$. Проверьте еще раз.

Да, конечно. Поправил (просто старое скопировал).

Небольшой перебор дал ещё вот такое:

$\sqrt[3]{1+\sqrt[3]{-6860}} = \sqrt[3]{\frac{5}{9}}-\sqrt[3]{\frac{100}{9}}-\sqrt[3]{\frac{16}{9}}$

Интересно отметить, что $6860$ почти полный куб: $6860=19^3+1$

[nnosipov]

Да, есть такой пример.

Rak so dna в сообщении #1702716 писал(а):

Интересно отметить, что $6860$ почти полный куб: $6860=19^3+1$

Видимо, любое такое $a$ априори должно иметь вид $a=k^3-1$ для некоторого целого $k$, но я что-то не вижу простого объяснения этому.

[Rak so dna]

Всё, что смог:

Нам надо найти все целые $a,x,y$, для которых

$27xy(x+y)\left(x^2+xy+y^2\right)^3 = a\left(y^3+6xy^2+3x^2y-x^3\right)^3$

Положим $a=n^3+1$ тогда:

\begin{align*} &27xy(x+y)\left(x^2+xy+y^2\right)^3 - a\left(y^3+6xy^2+3x^2y-x^3\right)^3=\\ &\Bigl((n+1)x^3-3(n-2)yx^2-3(2n-1)y^2x-(n+1)y^3\Bigr)\cdot\\ &\left(\frac{3}{4}\Bigl[y^3-3xy^2-6x^2y-x^3\Bigr]^2 + \frac{1}{4}\Bigl[(2n-1)x^3-6(n+1)yx^2-3(4n+1)y^2x-(2n-1)y^3\Bigr]^2 \right) \end{align*}

(maxima code)

f(t) := 27*(x^2+x*y+y^2)^3*x*y*(x+y) - (n^3+1)*(y^3+6*x*y^2+3*x^2*y-x^3)^3;

r(t) := 
((n+1)*x^3-3*(n-2)*y*x^2-3*(2*n-1)*y^2*x-(n+1)*y^3)*
( 3/4*(y^3-3*x*y^2-6*x^2*y-x^3)^2 +  1/4*((2*n-1)*x^3-6*(n+1)*y*x^2-3*(4*n+1)*y^2*x-(2*n-1)*y^3)^2) ;

rat( f(t) - r(t) );

Отсюда видно, что целые корни может иметь лишь первый множитель, и потому $a$ обязан иметь вид $n^3+1$.

Если подбирать $n$, то при "правильных" значениях, многочлен $(n+1)x^3-3(n-2)yx^2-3(2n-1)y^2x-(n+1)y^3$ должен развалиться на линейные множители.

Если же подбирать $x,y$, то должна быть целой дробь $\dfrac{x^3+6x^2y+3xy^2-y^3}{y^3+6y^2x+3yx^2-x^3}$

Ну и отношение $\dfrac{x}{y}$ при $n\rightarrow\pm\infty$, стремится к одному из корней уравнения $t^3-3t^2-6t-1=0$ (можно выбрать любой), что должно облегчить перебор.