Я разбираюсь с понятием (линейной) комплексной структуры на вещественных векторных пространствах. Мне встретился в Википедии пример, который мне не совсем понятен.
Вот мой перевод с английского:
Совокупность

вещественных матриц
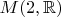
над полем вещественных чисел является 4-мерным. Для любой матрицы
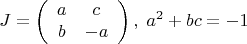
ее квадрат совпадает с минус единичной матрицей. Комплексная структура может быть построена в
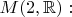
если

- единичная матрица, элементы
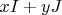
с матричным умножением образуют комплексные числа.
Мне непонятно построение комплексной структуры:

и

- здесь вещественные числа?
Я знаю, что имеется взаимно однозначное соответствие между квадратными матрицами порядка 2 и комплексными числами
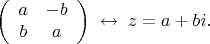
Мне непонятно построение комплексной структуры. При рассмотрении
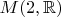
как 4-мерного пространства, векторы - это матрицы, поле скаляров -

(с очевидным базисом). При построении комплексной структуры мы получили 2-мерное пространство с базисом, состоящим из матриц

и
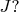
Элементами этого пространства являются матрицы вида
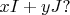
Почему мы теперь рассматриваем матричное умножение?