Математическая трактовка ММИ

[B3LYP]

Если я правильно понимаю, в ММИ любая ВФ, которая представлена суммой а не одночленом, говорит о "расщеплении вселенных", и каждый член в этой сумме как бы представляет отдельную вселенную. Хотелось бы лучше понимать, как это расщепление описывается математически. Возьмём классическую задачу на движение частицы при наличии потенциального барьера (тоннельный эффект). Можно говорить, что если частица пройдёт через барьер - это первая вселенная, а если отскочит от барьера и полетит назад - это вторая вселенная?
В очередной раз пересмотрел видео про барьер с канала Professor Dave explains:

https://youtu.be/EMq_QbyghMU
https://youtu.be/kUR98x1tH0c

Мы имеем движущуюся в одномерном пространстве частицу, потенциальная энергия равна 0 при $x<0$ и $x>a$, и равна $U_0$ при $0<x<a$.

Дейв рассказывает, что решение УШ будет выглядеть так:

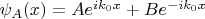
$\psi_{A}(x)=Ae^{ik_0x}+Be^{-ik_0x}$ при $x<0$

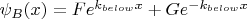
$\psi_{B}(x)=Fe^{k_{below}x}+Ge^{-k_{below}x}$ при $0<x<a$

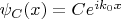
$\psi_{C}(x)=Ce^{ik_0x}$ при $x>a$

$k_0=\frac{\sqrt{2mE}}{\hbar}$
$k_{below}=\frac{\sqrt{2m(U_0-E)}}{\hbar}$

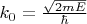
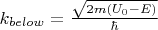
В данном случае энергия частицы меньше энергии барьера $U_0$.
Далее Дэйв решает это УШ через задание граничных условий, и получает формулу для коэффициента отражения $B^2/A^2$.
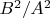
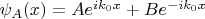
Я по-прежнему не понимаю, что вообще означает такое решение, когда не видно различия между прошлым и будущим, а ещё не понимаю как в рамках ММИ трактовать разные участки волновой функции. Тем не менее, можно ли грубо сказать, что для $x<0$ решение $\psi_{A}(x)=Ae^{ik_0x}+Be^{-ik_0x}$ это вроде как две вселенные, первое слагаемое отвечает первой плюс второй вселенной (в первой частица пролетела сквозь барьер), а второе второй?

[realeugene]

B3LYP в сообщении #1702067 писал(а):

Хотелось бы лучше понимать, как это расщепление описывается математически.

В статье Эверетта есть строгая математика.

B3LYP в сообщении #1702067 писал(а):

Можно говорить, что если частица пройдёт через барьер - это первая вселенная, а если отскочит от барьера и полетит назад - это вторая вселенная?

И близко нет.

[Утундрий]

Риторический вопрос: зачем плодить однотипные темы без какой либо спецификации?

[B3LYP]

realeugene в сообщении #1702081 писал(а):

И близко нет.

Почему?
А если электрон, летящий влево, вызывает срабатывание детектора, который запускает яд в коробку и убивает кота Шредингера?

[realeugene]

B3LYP в сообщении #1702101 писал(а):

Почему?

Потому что эти фантазии по мотивам очень далеки от ММИ. Ссылка на первоисточник в соседней теме.