Вот здесь в другой теме Вы писали:
То есть прогноз для этого интервала был: 9.527 кортежей 17-240-1 (центральных 17-к), а вовсе не 21 и не 20. Мы с Демисом недавно закончили проверку этого интервала и нашли в нём 11 центральных 17-к.
Таким образом, здесь относительная ошибка прогноза
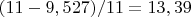
% послу учета 13 коэффициентов.
Рассмотрим другой пример. Возьмем паттерн
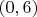
. По формуле Х-Л на диапазоне до

(по формуле с одним интегралом, т.е. по-вашему с коэффициентом

) количество кортежей равно
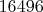
. Реальное же число "чистых" кортежей на данном диапазоне
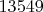
.
Подсчитаем мат. ожидание расстояния между такими кортежами
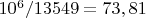
и
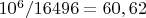
, т.е. относительная ошибка
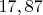
%. Не очень большая для прогноза с одним коэффициентом. Сравнительно небольшая относительная ошибка связана с большим хвостом распределения Пуассона.