Но возможно, известен закон распределения и как выглядит дисперсия для этого закона,
Нет, закон распределения не известен — ни плотность, ни вид. Я точно знаю только математическое ожидание

(истинное значение) и то, что случайная величина лежит на отрезке
![$[-1, M]$ $[-1, M]$](https://dxdy-01.korotkov.co.uk/f/4/1/f/41f56b19eb701ed7a03731de83d5060482.png)
. Причем распределение может быть как дискретным, так и непрерывным — информации о виде распределения нет. Я рассматриваю оба варианта.
Выборка может быть достаточно большой — от 10 000 до 10 000 000 наблюдений. Значение

можно определить, но не всегда — поэтому хотелось бы иметь метод, позволяющий оценивать дисперсию

и одновременно понимать погрешность этой оценки.
Сейчас я пытаюсь подобрать возможные распределения только для симуляций, чтобы протестировать разные методы и посмотреть, какой точности удается достичь при оценке дисперсии.
---
MAD-оценки известная штука, можете, например, здесь почитать
https://disk.yandex.ru/i/RCGkshn3Sjd-xw Спасибо, буду изучать!
---
Вопрос остался: так вам известен вид распределения (того, которое с тяжелыми хвостами), плотность, скажем?
Нет, вид распределения неизвестен. Есть только гипотезы, какие распределения могут быть похожи на реальное — их я использую для тестовых симуляций.
---
И правильно я понимаю ваш последний пост, что матожидание тоже неизвестно, только оценка?
Нет, математическое ожидание

известно точно. Также можно определить максимальное значение

с точностью 100%. Случайная величина принимает значения в диапазоне
![$[-1, M]$ $[-1, M]$](https://dxdy-01.korotkov.co.uk/f/4/1/f/41f56b19eb701ed7a03731de83d5060482.png)
.
Цель: по выборке размера

и известному

как можно точнее оценить дисперсию

и понять погрешность этой оценки.
---
откуда уверенность в тяжелых хвостах?
Просто известно, что случайная величина
![$\u \in [-1, M]$ $\u \in [-1, M]$](https://dxdy-02.korotkov.co.uk/f/d/7/a/d7a9e701188540eb0c2f7510f25bceb582.png)
распределена так, что чаще встречаются отрицательные или небольшие положительные значения, но иногда — редкие и большие значения вплоть до

. Именно они образуют тяжелый хвост распределения.
---
И вот еще осталось. Как вы хотите считать погрешность оценки?
Пока точно не знаю. Но для меня важно понимать погрешность, чтобы оценивать надежность методов. Например, если окажется, что погрешность оценки дисперсии составляет 50%, то такой метод использовать смысла нет.
---
Сейчас я сделал тестовую модель. Для симуляций я использовал дискретное распределение
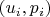
с
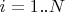
, где

брал от 10 до 20 и задавал
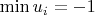
и
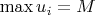
, а вероятности

убывают по геометрической прогрессии: значение

встречается чаще всего,

— реже всего.
Я построил метод оценки

через два момента:
1.
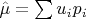
— среднее по выборке без редкого максимального значения

,
2.
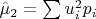
— второй момент по той же выборке.
Далее я вывел формулу:
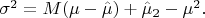
Она получается из двух уравнений:
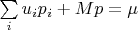
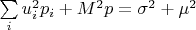
В моих тестах данного метода относительная ошибка для дисперсии составила примерно 10%, что пока не знаю — много это или мало.
Следующий шаг — построить непрерывное распределение на
![$[-1, M]$ $[-1, M]$](https://dxdy-01.korotkov.co.uk/f/4/1/f/41f56b19eb701ed7a03731de83d5060482.png)
с заданными

и

, сгенерировать выборку и проверить точность метода. Если ошибка снова будет около 10%, буду думать, как улучшить точность.
Если есть идеи, как построить более точную оценку дисперсии с контролем погрешности — буду рад советам.