Халяльные решения волнового уравнения

[Утундрий]

В этой теме я планирую провентилировать взаимную обусловленность таких хороших/годных свойств решений некоторых УрЧП, как ограниченность, конечность действия и конечность энергии.

Начнём с чего-нибудь простенького.

Рассмотрим функцию двух переменных $\phi(t,x)$, заданную на всём $\mathbb{R}^2$ и являющуюся экстремалью функционала действия:

$$S \equiv \frac 1 2 \iint\limits_{-\infty}^{\quad\;+\infty} dt\wedge dx \left[\left(\phi_t\right)^2-\left(\phi_x\right)^2\right] \eqno (1)$$

Для этого она должна удовлетворять волновому уравнению:

$$\phi_{tt}=\phi_{xx} \eqno (2)$$

общее решение которого имеет вид

$$\phi(t,x)=a(x+t)+b(x-t) \eqno (3)$$

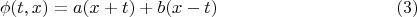
где $a$ и $b$ — произвольные дважды дифференцируемые функции одной переменной.

Отсюда видно, что ограниченность $\phi$ (и её частных производных) равносильна ограниченности функций $a$ и $b$ (и их обыкновенных производных).

Численное значение действия $(1)$ проще всего найти, переходя к повёрнутым координатам:

$$\left\{ {\begin{array}{l} u=x+t \\ v=x-t \\ \end{array} } \right. $$

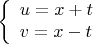
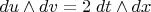
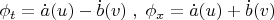
Поскольку $du \wedge dv = 2\; dt \wedge dx$ и $\phi_t=\dot a(u)-\dot b(v)\; , \; \phi_x=\dot a(u)+\dot b(v)$, находим

$$S = - \iint\limits_{-\infty}^{\quad\;+\infty} du\wedge dv \; \dot a(u) \; \dot b(v)=- \int\limits_{-\infty}^{\;+\infty} du\; \dot a(u) \int\limits_{-\infty}^{\;+\infty} dv\; \dot b(v)$$

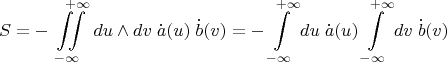
Возникшие несобственные интегралы сходятся, когда функции $a$ и $b$ имеют конечные пределы на бесконечности. Обозначим эти пределы так:

$$a_{\pm} \equiv \lim_{x \to \pm \infty} a(x)\; , \quad b_{\pm} \equiv \lim_{x \to \pm \infty} b(x) \eqno (4)$$

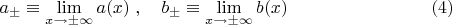
Тогда для действия получаем следующую формулу:

$$S=-\left(a_{+}-a_{-}\right)\left(b_{+}-b_{-}\right) \eqno (5)$$

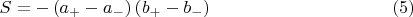
Поэтому конечность действия равносильна существованию пределов $(4)$.

Переходим к энергии:

$$E(t) \equiv \frac 1 2 \int\limits_{-\infty}^{\;+\infty} dx \left[\left(\phi_t\right)^2+\left(\phi_x\right)^2\right] \eqno (6)$$

Подставляя сюда $(3)$, находим

$$E(t) = \int\limits_{-\infty}^{\;+\infty} dx \left[\dot a(x)^2+\dot b(x)^2\right] = const \eqno (7)$$

Откуда видно, что конечность энергии равносильна сходимости следующих несобственных интегралов:

$$ \int\limits_{-\infty}^{\;+\infty} dx \; \dot a(x)^2 < \infty\; , \quad \int\limits_{-\infty}^{\;+\infty} dx \; \dot b(x)^2 < \infty \eqno (8)$$

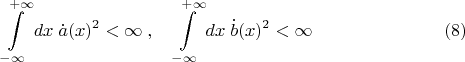
Глядя на всё это многобезобразие у меня возникает ощущение, что рассмотренные три свойства (ограниченность, конечность действия и конечность энергии) крайне слабо связаны друг с другом. Я прав?

[Утундрий]

Введём класс функций $\mathcal{B}^k_{\alpha \beta}(\mathbb{R})$, где $k=0,1,2 \ldots \infty \; ; \quad \alpha, \beta \in \{ 0,1\}$.

$f(x)\in \mathcal{B}^k_{\alpha \beta}(\mathbb{R})$ согда выполнены следующие условия:

$${1^°} \quad f(x) \in C^k(\mathbb{R})$$

$${2^°} \quad \sup_{x \in \mathbb{R}} |f^{(s)}(x)| < \infty \; , \quad s=0,1,2 \ldots k$$

$${3^°} \quad \sup_{x \in \mathbb{R}} |f^{(k+1)}(x)| = \infty \; \text{при}\; k<\infty$$

$${4^°} \quad \lim_{x \to \pm \infty} f(x)<\infty \;\text{ при} \; \alpha =1$$

$${5^°} \quad \lim_{x \to \pm \infty} f(x)=\infty \;\text{ при} \; \alpha =0$$

$${6^°} \int\limits_{-\infty}^{\;+\infty} dx \; \dot f(x)^2 < \infty\;\text{ при}\; \beta =1$$

$${7^°} \int\limits_{-\infty}^{\;+\infty} dx \; \dot f(x)^2 = \infty\;\text{ при}\; \beta =0$$

То есть, $\alpha$ отвечает за конечность действия, а $\beta$ за конечность энергии. Переберём все возможные комбинации этих факторов и сочиним каждому набору по представителю:

$$ 1 \in \mathcal{B}^{\infty}_{1 1}(\mathbb{R})$$

$$\sin x \in \mathcal{B}^{\infty}_{0 0}(\mathbb{R})$$

$$\dfrac {\sin x}{1+|x|^{1/2}} \in \mathcal{B}^{\infty}_{1 0}(\mathbb{R})$$

$$\ln (1+x^2) \in \mathcal{B}^{\infty}_{0 1}(\mathbb{R})$$

Теперь, чтобы понизить степень гладкости-ограниченности, рассмотрим функцию

$$f_k(x)\equiv \dfrac {\sin(x^{k+1})}{x} e^{-x^2}$$

которая лежит в $C_b^{k}(\mathbb{R})$, но не в $C_b^{k+1}(\mathbb{R})$ и настолько быстро убывает на бесконечности, что её прибавление оставляет свойства $\alpha$ и $\beta$ без изменения:

$$ 1 + f_k(x) \in \mathcal{B}^k_{1 1}(\mathbb{R})$$

$$\sin x + f_k(x) \in \mathcal{B}^k_{0 0}(\mathbb{R}) $$

$$\dfrac {\sin x}{1+|x|^{1/2}}+ f_k(x) \in \mathcal{B}^k_{1 0}(\mathbb{R})$$

$$\ln (1+x^2)+ f_k(x) \in \mathcal{B}^k_{0 1}(\mathbb{R})$$

Итак, если я правильно понимаю науку логику, можно констатировать, что все три рассмотренные свойства являются полностью независимыми.

[Утундрий]

Возражений нет, что внушает робкую надежду на то, что мне удалось избежать хотя бы слишком уж очевидных ошибок. Посему закруглю первую мелодию, прежде чем переходить по второму (действительно интересующему меня) уравнению.

Дело в том, что редко кто рассуждает в терминах профилей бегущих волн. Обычно в ход идёт задача Коши:

$$\left\{ {\begin{array}{rcl} \phi(0,x)&=&\varphi (x) \\ \phi_t (0,x)&=&\psi (x) \\ \end{array} } \right. \eqno (9)$$

Её решение даётся формулой

$$\phi (t,x)=\frac 1 2 \left[ \varphi (x+t) +\varphi (x-t) \right] +\frac 1 2 \int\limits_{x-t}^{x+t} \psi (\xi) \; d \xi \eqno (10)$$

Что можно реализовать следующим выбором профилей волн:

$$2\; a(x)=\varphi(x)+\int\limits_{0}^{x} \psi (\xi) \; d \xi \; , \quad 2\; b(x)=\varphi(x)-\int\limits_{0}^{x} \psi (\xi) \; d \xi$$

Тогда

$$4\;S={\langle \psi \rangle}^2-(\varphi_{+}-\varphi_{-} )^2 \eqno (11) $$

где

$$\langle \psi \rangle \equiv \int\limits_{-\infty}^{\;+\infty} \psi (x) \; d x \; , \qquad \varphi_{\pm} \equiv \lim_{x \to \pm \infty} \varphi(x) \eqno (12)$$

А для энергии получается следующее выражение:

$$E =\frac 1 2 \int\limits_{-\infty}^{\;+\infty} dx \left[\dot \varphi(x)^2+\psi (x)^2\right] \eqno (13)$$

Отсюда понятно что и куда налагать, чтобы получить нечто желаемое. Не буду разжёвывать.

[Red_Herring]

Все вроде правильно и, на мой взгляд, неинтересно. Почему? Потому что волновое уравнение одномерное и сводится к двум бегущим волнам, поэтому имеется хорошо поставленность и в $ C^s$ и в $L^p$ $(0<p\le \infty)$ и связанных с ними и еще в куче пространств. А если пространсвенных переменных 2 и больше, то будет хорошая поставленность только в $L^2$, а в других не будет из-за фокусировки/расфокусировки

[Утундрий]

Red_Herring в сообщении #1696454 писал(а):

если пространсвенных переменных 2 и больше, то будет хорошая поставленность только в $L^2$, а в других не будет из-за фокусировки/расфокусировки

Я этого пока не понимаю, так что интересно будет обсудить. Поскольку 3D мне всяко не избежать. Но перед этим будет ещё один игрушечный пример.

[Утундрий]

Я сейчас немного завис. Поэтому что там насчёт

Red_Herring в сообщении #1696454 писал(а):

фокусировки/расфокусировки

?

[Red_Herring]

Рассмотрите сферическую волну в размерности 3 (там все самое простое) $u(r,t)=r^{-1} \bigl( f(r+ct) - f(r-ct)\bigr)$. И в качестве $f$ ступенька.

[Утундрий]

А, то есть смысл просто в том, что имплозия гладкого распределения может дать особенность?

[Red_Herring]

Утундрий в сообщении #1700105 писал(а):

А, то есть смысл просто в том, что имплозия гладкого распределения может дать особенность?

Я не совсем понимаю, что это такое имплозия, но смысл в общем-то такой. Фокусировка это предельный случай и особенность самая сильная. Регулярные каустики это самый слабый случай. И есть промежуточные.

[Утундрий]

Red_Herring в сообщении #1700106 писал(а):

что это такое имплозия

Взрыв внутрь. Термин стал более-менее на слуху после эпик-фейла парочки миллиардеров, необратимо занырнувших к "Титанику" в собранном на коленке композитном ведре.

[Red_Herring]

Утундрий в сообщении #1700120 писал(а):

Взрыв внутрь

А взрыв наружу это эксплозия? На самом деле нечто подобное происходит: быстро осциллирующее решение имеет вид

$$u(\boldsymbol{x},t, k)\sim \sum_{n=0}^\infty A_n \boldsymbol{x},t) e^{i\varphi (\boldsymbol{x},t)k} k^{-n}$$

Оно не глобальное, до появления "имплозии" proeкции фазового потока на координаты и вот

$$A_0 \asymp |\frac{D ( \boldsymbol{y})} {D ( \boldsymbol{x})} |^{-1/2}$$

и поэтому в $L^2$ все кошерно, норма решения сохраняется, в $L^p$ с $p>2$ происходит потеря в момент катастрофы фазового потока, т.е. норма становится очень большой, а вот с $p<2$ норма становится очень маленькой, сиречь имплозия, т.е. эксплозия в противоположном времени

[Утундрий]

Следующим ну́мером идёт уравнение

$$\phi_{tt}-\phi_{xx}+\frac {2}{\operatorname{ch}^2 t}\; \phi =0$$

Для него придётся решить практически все те же задачи, кроме конечности энергии, поскольку никакой внятно сохраняющейся энергии тут нет.

Было бы небесполезно для дальнейшего обсуждения, когда бы не́кто превентивно сказану́л бы не́что относительно анонсируемого.

[Red_Herring]

Утундрий в сообщении #1700351 писал(а):

Для него придётся решить практически все те же задачи, кроме конечности энергии, поскольку никакой внятно сохраняющейся энергии тут нет.

Сохраняющейся энергии нет, а вот конечность энергии

$$E(t):=\int _{-\infty}^\infty \bigl(u_t^2 + u_x^2+ \cosh^{-2}(t) u^2 \bigr)\,dx $$

вычисленной в любой момент времени вполне может быть. Более того, это выражение убывает при $t>0$ и возрастает при $t<0$.

[Утундрий]

Всё равно возникает вопрос — почему именно это выражение? Можно вместо чёсинуса поставить любую возрастающую функцию $t$ и тоже получится нечто "асимптотически сохраняющееся". Или конкретно эта величина как-то "более сохраняется" нежели остальные? Мне это не очевидно, так что предпочту вовсе с нею не связываться.

[Red_Herring]

Ну потому что умножая уравнение на $2u_t $ и интегрируя по $x$ мы получим ...