EminentVictoriansНу в Вашем примере на скриншоте вполне обычное рассуждение, только записанное без использования слов. Логика там та же самая, что и у Вас. Вас просто напугала эта громоздкость, а если не пугаться, а просто посмотреть внимательнее и разобраться, то можно даже получить от этого удовольствие. Но тут, конечно, уж слишком подробно всё расписано, это запись не для человека, а для компьютера. Важно, что можно было бы то же рассуждение написать и короче, с использованием слов, и всё равно имея в виду про себя использование аксиом логики. То есть тут не логика "нечеловеческая", а просто запись не очень человеческая, слишком скрупулёзная.
(1) означает, что существует пустое множество

, которому ничего не принадлежит. Это аксиома.
(2)-(5) означает, что если какое-то множество

равно этому пустому множеству

, то игреку тоже ничего не принадлежит - просто по смыслу равенства. Замечу, что если в доказываемом утверждении (25) вместо

написать

, то фрагмент (2)-(5) не потребуется, а смысл будет всё равно почти тот же самый.
Дальше и до самого конца идёт доказательство, что и наоборот, если какому-то множеству ничего не принадлежит, то оно равно нашему пустому множеству

- это и значит, что нет двух пустых множеств. То есть из предположения (6) надо вывести

. В свою очередь, для этого сначала в (7)-(10) доказывается, что если какой-то элемент

принадлежит

, то он принадлежит и

(просто потому что по предположению игреку не может ничего принадлежать, а из лжи следует что угодно), а затем в (11)-(14) так же доказывается, что и наоборот, из принадлежности

следует принадлежность

. Дальше в (15)-(20) на основании этого получается, что

, со ссылкой на аксиому экстенсиональности (если два множества состоят из одних и тех же элементов, то они равны). Содержательная часть доказательства на этом закончена, дальше просто происходит формирование доказываемого утверждения в том виде, в каком оно должно быть.
Словами то же самое доказательство я бы изложил так. По аксиоме пустого множества, существует пустое множество

. Докажем, что если
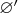
тоже пустое, то
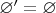
. В самом деле, из
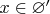
(как из заведомой лжи) следует

, и наоборот. По аксиоме экстенсиональности
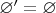
. Значит, пустое множество единственно.
Для меня это одно и то же доказательство, только по-разному записанное, и логика тут одна и та же. Ваше доказательство немного другое, от противного, его тоже можно было бы записать формально, и от этого логика в нём бы не изменилась.