База просчитанных случаев стала слишком большой.
Сегодня обнаружил, что 3-й день ищу цепочку из 8-и чисел по 588 делителей, которую я, оказывается уже нашел (причем не 3 года, а менее месяца тому назад, и не за три дня, а за один)

Причем я даже опубликовал начальное число цепочки и обновил данные в одной из таблиц, куда заношу все результаты. А в другой - забыл. И именно на основании другой таблицы приступил к повторному поиску.
Дабы впредь избежать подобных эксцессов я ... изготовил еще одну таблицу

Речь идет только о длинных цепочках.
В процессе наполнения нашел кое-какие странности. Например, нашлась готовая программа для
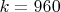
(с виду, вполне берущийся случай), а следов запуска этой программы я не обнаружил.
Есть и другие вопросы. Так, насколько я помню, поиск цепочки длиннее 11 для

интенсивно проводился (скорее всего Евгением), но искать подтверждение этому в дву с лишним сотнях страниц темы = убить еще полдня.
В общем, буду благодарен за любые уточнения и исправления (табличка сырая).
Кстати, я внес туда не только

, для которых есть длинные цепочки, но и перспективные.