Можно ли, используя только цифры 2, 3, 4, 9, составить два натуральных числа, одно из которых в 44 раза больше другого?
Нет, нельзя.
Рассуждение можно строить рассматривая последовательно возможные цифры единиц, десятков и т.д.
Для единиц допустимая последняя цифра (единиц) только 3, и
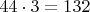
, т.е. десятков уже будет

Эти 13 складываем с десятками от второй справа цифры (десяток),
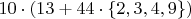
смотрим что получается. И так далее.
Но можно построить сколь угодно большое ("бесконечное") число, и если произведение его на 44 читать с младших разрядов, то может получиться так:
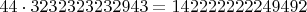
Повторяя "32" сколь угодно много раз ("бесконечно") в старших разрядах, мы получим только допустимые цифры в младших разрядах, ну и единицу в самом старшем, которая портит всю малину.