Количество слагаемых в разложении степени двучлена

[cxzbsdhwert]

Утундрий в сообщении #1698564 писал(а):

cxzbsdhwert в сообщении #1698562 писал(а):

Конечная формула, если Вы не читали следующие за первым сообщения, получилась такая:

$$\frac{2n(2n-2\cdot 1)...(2n-2\cdot(n-1))}{n!}$$

Вынесите двойку из каждой скобки...

Зачем? Вы читали сообщения выше?

[Утундрий]

cxzbsdhwert в сообщении #1698566 писал(а):

Зачем?

Чтобы привести эту корявую формулу к более компактному виду.

[Someone]

cxzbsdhwert в сообщении #1698566 писал(а):

Зачем? Вы читали сообщения выше?

То, что Вы делаете — это просто ужас какой-то. Особенно ввиду https://dxdy.ru/post1698515.html#p1698515. Всё-таки сделайте то, о чём Вас просят:

Утундрий в сообщении #1698564 писал(а):

Вынесите двойку из каждой скобки...

[cxzbsdhwert]

Утундрий в сообщении #1698568 писал(а):

cxzbsdhwert в сообщении #1698566 писал(а):

Зачем?

Чтобы привести эту корявую формулу к более компактному виду.

В моём сообщении к Вам был ещё вопрос — читали ли Вы предыдущие сообщения. Если под компактным видом, Вы имели в виду $\dfrac{2^nn!}{n!}$ или $2^n$, то это было выше расписано.

А формула не корявая, а более подробная и дающее больше понимая того, что происходит

-- 17.08.2025, 22:07 --

Someone в сообщении #1698577 писал(а):

cxzbsdhwert в сообщении #1698566 писал(а):

Зачем? Вы читали сообщения выше?

То, что Вы делаете — это просто ужас какой-то. Особенно ввиду https://dxdy.ru/post1698515.html#p1698515. Всё-таки сделайте то, о чём Вас просят:

Утундрий в сообщении #1698564 писал(а):

Вынесите двойку из каждой скобки...

Дак я ведь в сообщении, на которое Вы ссылаетесь это и сделал. Или я что-то не понимаю?

[Утундрий]

cxzbsdhwert в сообщении #1698579 писал(а):

формула не корявая, а более подробная и дающее больше понимая того, что происходит

[cxzbsdhwert]

Утундрий в сообщении #1698581 писал(а):

cxzbsdhwert в сообщении #1698579 писал(а):

формула не корявая, а более подробная и дающее больше понимая того, что происходит

Смайлики это не конструктивно, но всё равно спасибо всем за помощь

[Combat Zone]

cxzbsdhwert в сообщении #1698562 писал(а):

Всё сходится. Конечная формула, если Вы не читали следующие за первым сообщения, получилась такая:

Интересно девки пляшут. Отродясь было четыре, а тут вдруг 8. Это вы не то считаете. Это вас ахи разные и бэхи разные.
Но если не хотите сокращать, - я гляжу, вам не понравилось предложение, - то воля ваша, носите эту страшную дробь. А вопрос-то в чем?

[cxzbsdhwert]

Combat Zone в сообщении #1698584 писал(а):

cxzbsdhwert в сообщении #1698562 писал(а):

Всё сходится. Конечная формула, если Вы не читали следующие за первым сообщения, получилась такая:

Интересно девки пляшут. Отродясь было четыре, а тут вдруг 8. Это вы не то считаете. Это вас ахи разные и бэхи разные.
Но если не хотите сокращать, - я гляжу, вам не понравилось предложение, - то воля ваша, носите эту страшную дробь. А вопрос-то в чем?

Вы наверное тоже не прочитали предыдущие сообщения — интересовало число одночленов с единичным коэффициентом.
Извините, давайте продолжим завтра, если ещё есть вопросы

[Combat Zone]

cxzbsdhwert в сообщении #1698586 писал(а):

Извините, давайте продолжим завтра, если ещё есть вопросы

Не, завтра понедельник. Вопросов нет, оно вам надо. И я про одночлены с единичным к-том. Сейчас напишу, что вы считаете.

-- 17.08.2025, 22:29 --

А считаете вы число слагаемых, если раскрыть скобки вот тут:
$(a_1+b_1)\cdots (a_n+b_n)$.

-- 17.08.2025, 22:31 --

cxzbsdhwert в сообщении #1698586 писал(а):

интересовало число одночленов с единичным коэффициентом.

Но можно и так. Это одно и то же.

-- 17.08.2025, 22:34 --

Надо отдать вам должное, придумать проблему на ровном месте и ее пытаться решить... а можно спросить, зачем? А если у вас будет бином $(a+1.5b)^n$, так это ж страшно спросить, что вы будете считать и что сочтете в роли конечного результата.

[maxmatem]

Если я правильно понял ТС , он просто хотел посчитать сколько всего слагаемых в непричесанном разложении $(a+b)^{n}$

разложение назовём непричесанным если в этом разложении не приводили подобные слагаемые .

(Оффтоп)

Да уж …

[cxzbsdhwert]

Combat Zone в сообщении #1698587 писал(а):

придумать проблему на ровном месте и ее пытаться решить... а можно спросить, зачем? А если у вас будет бином $(a+1.5b)^n$, так это ж страшно спросить, что вы будете считать и что сочтете в роли конечного результата.

"Придумать проблему" или "найти проблему", ну это уже философский вопрос, сводящиеся к "открывают ли математику или изобретают?".
Решение этой задачи, полагаю, имеет прикладное прикладное значение, но меня интересует решение как таковое, как минимум с точки зрения обучения.
Ну а Вы и другие пользователи с этой страницы, по-моему всё-таки просто не прочитали сообщения с первой страницы, где уже всё разобрали.

[Someone]

cxzbsdhwert в сообщении #1698605 писал(а):

Решение этой задачи, полагаю, имеет прикладное прикладное значение, но меня интересует решение как таковое, как минимум с точки зрения обучения.

Эта задача имеет чрезвычайно простые и короткие решения, которые Вам пытались подсказать: https://dxdy.ru/post1698517.html#p1698517, https://dxdy.ru/post1698524.html#p1698524, https://dxdy.ru/post1698561.html#p1698561. И с точки зрения обучения они лучше. Поверьте человеку, который более 40 лет преподавал математику студентам.

[cxzbsdhwert]

Someone в сообщении #1698636 писал(а):

cxzbsdhwert в сообщении #1698605 писал(а):

Решение этой задачи, полагаю, имеет прикладное прикладное значение, но меня интересует решение как таковое, как минимум с точки зрения обучения.

Эта задача имеет чрезвычайно простые и короткие решения, которые Вам пытались подсказать: https://dxdy.ru/post1698517.html#p1698517, https://dxdy.ru/post1698524.html#p1698524, https://dxdy.ru/post1698561.html#p1698561. И с точки зрения обучения они лучше. Поверьте человеку, который более 40 лет преподавал математику студентам.

А я и не спорил, что другие решения также представляют ценность. Не знаю чем вообще вызвано, как мне показалось, недовольство отвечающих.

Единственное в чём, может быть, мнения отличаются, это в том, что наиболее интуитивное, объясняющее "что и как" решение всё-таки, по моему мнению, приведено мной - другие решения, как Вы сами написали - чрезвычайно короткие. post1698517.html#p1698517 например конечно ультра-очевидное, спасибо за подсказку, но мало-что объясняющее само по себе.

Думаю, что этот спор не заслуживает ничьего внимания и не важен, поэтому, предлагаю не раздувать тему, всем ещё раз спасибо.

[Someone]

cxzbsdhwert в сообщении #1698704 писал(а):

конечно ультра-очевидное, спасибо за подсказку, но мало-что объясняющее само по себе.

Дык, там (во всех трёх случаях) всего несколько слов надо добавить, а не заставлять ученика гадать, откуда это взялось. А то, что Вам написали — это просто подсказки, соответствующие правилам форума: не давать спрашивающему готового решения.
А что Вы будете делать, если понадобится подсчитать, сколько будет слагаемых в $(a_1+a_2+\ldots+a_m)^n$, если раскрыть скобки и не приводить подобные члены? Те решения, которые пытались Вам подсказать, легко обобщаются на этот случай и мгновенно дают результат.

[wrest]

cxzbsdhwert в сообщении #1698704 писал(а):

например конечно ультра-очевидное, спасибо за подсказку, но мало-что объясняющее само по себе.

У вас есть несколько групп (группа - слагаемые в скобках), вам надо узнать сколько будет комбинаций "каждый член одной группы с каждым из других групп)".
Так это ж просто произведение количеств членов каждой группы.
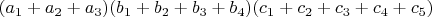
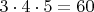
Если у вас положим три группы по 3,4,5 членов в каждой: $(a_1+a_2+a_3)(b_1+b_2+b_3+b_4)(c_1+c_2+c_3+c_4+c_5)$, то всего будет $3\cdot 4 \cdot 5=60$ комбинаций (слагаемых) вида $a_i b_j c_k$.
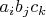
Это ж прям вот очевидно. Если 10 групп по 2 члена, то будет $2^{10}$ комбинаций. Если 2 группы по 10 членов, то $10^2$ комбинаций...
Прямое произведение, зачем тут факториалы и прочее?