Доказать, что тор, полученный вращением вокруг оси

окружности
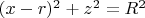
, где

, является гладким двумерным вложенным многообразием.
Вроде тут просто определения надо было проверить. Всё ли я правильно сделала?
Тор можно задать параметрически с помощью углов

(вращение вокруг оси

) и

(угол на окружности):
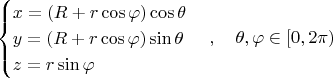
где

— расстояние от центра тора до центра окружности,

— радиус окружности (

).
Гладкость параметризации:
Функции
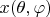
,
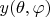
,
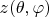
бесконечно дифференцируемы по

и

, так как являются композициями тригонометрических функций.
Регулярность параметризации:
Матрица Якоби:
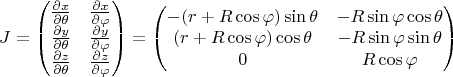
Ранг

равен 2 для всех

, так как векторы:
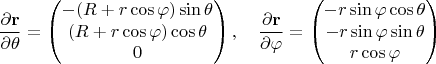
линейно независимы (их векторное произведение не обращается в ноль).
Уравнение:
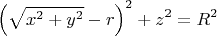
Раскрывая скобки:
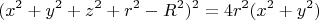
Градиент функции
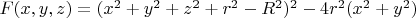
:
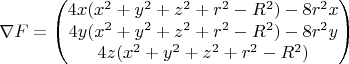
На торе (

) градиент
не обращается в ноль, что гарантирует гладкость поверхности (по теореме о неявной функции).
Вложение в

:
Параметризация инъективна на
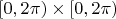
с отождествлением границ:
Точки
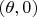
и
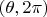
отображаются в одну точку
Точки
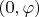
и
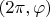
отображаются в одну точку
Это соответствует стандартной топологии тора как факторпространства квадрата.
Отображение параметризации собственное:
Прообраз любого компакта в

компактен в
![$[0, 2\pi] \times [0, 2\pi]$ $[0, 2\pi] \times [0, 2\pi]$](https://dxdy-01.korotkov.co.uk/f/c/0/2/c0226478897ae7991134ac492e8c24c882.png)
Следует из ограниченности тора и непрерывности параметризации
Параметризация инъективна на
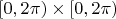
с отождествлением границ. Отображение собственное (прообразы компактов компактны). Таким образом, тор является гладким двумерным вложенным многообразием в

.