Я начал изучать алгебру по учебнику Aluffi. В начале даются простые понятия для введения в теорию категорий, но мне пока трудно с этим всем разбираться. Помогите, пожалуйста, разобраться.

Тут говорится, что мономорфизм это обобщение инъекции. Для чего в определении мономорфизма введены дополнительыне множества

и отображения
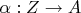
? Интуитивно не понятно, для чего так придумали.
Ниже по тексту дается задание догадаться, каким будет определение эпиморфизма (обобщение сюрьекции) и написать доказательство того, что функция сюрьективна тогда и только тогда, когда она эпиморфизм. Как можно доказать это утверждение?
-- 17.08.2025, 17:16 --Попробую предположить, что определение эпиморфизма будет такое: функция

называется эпиморфизмом, если выполняется следующее: для всех множеств

и всех функций
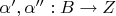
верно равенство