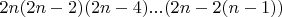У нас фактически

элементов -


ток и


ток.
С чего бы это вдруг? Объясните.
Число слагаемых в конечном итоге определяется тем, как написал пользователь b4b5, то есть размещение

элементов по

местам, но это, по всей видимости, частный случай более общей формулы комбинаторики, которую формулировал я.

скобок по 2 слагаемых в скобке. Сколько слагаемых? )
1. При возведении двучлена в степень

, будет

перемножающихся двучленов.
2. Каждый из двух членов

и

образует произведение с

остальных членов - со всеми такими же (

со всеми

, или

со всеми

), или частично с противоположным членом из других скобок (с

противоположными, с

противоположными и одним "своим" и т.д. до

противоположными и наоборот

"своим"), то есть

,

,

,

,

и т.д.
3. Тогда получается, что есть два множества из

элементов, состоящих из


и


соответственно, только каждый из

или

, не смотря на то, что это численно одни и те же элементы, различимы по критерию принадлежности к одной из

перемножаемых скобок. То есть

и

, или просто рассматривать их как разные числа со сквозной нумерацией
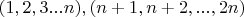
4. Поскольку, как написано выше, каждый из двух членов бинома образует произведение длинной в

множителей (включая себя) с остальными, а в биноме

члена, то получается, что рассматриваемых элементов всего

. Мы рассматриваем объединённое сквозное множество потому, что элементы из одного множества перемножаются и на элементы из другого (члены одного вида из каждой из

скобок, перемножаются и на члены второго вида из каждой скобки).
5. Каждое произведение, являющееся одним из слагаемых при раскрытии бинома, можно рассматривать как

ячеек, по которым размещаются

элементов.
6. Тогда задача сводится к тому, чтобы определить формулу для числа размещений

элементов по

местам, без повторений (чтобы не было

, то есть член из одной скобки на себя же не может умножиться), и без учёта порядка (
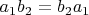
, но
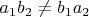
, поскольку, опять-таки, это одни и те же элементы с точки зрения численного значения, но разные с точки зрения того, в какой скобе они были).
Тогда получается, что в первую из

ячеек может быть размещён один из

элементов, вторым один из

, т.к. один мы уже использовали и он на себя не должен умножаться и т.д. до

. Из всех этих комбинаций из

элементов есть какое-то количество уникальных, с точки зрения порядка, на каждую из которых приходится какое-то число перестановок. Тогда нужно посчитать сколько может быть перестановок из

элементов, поделить на всё количество
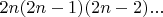
и получить число уникальных с точки зрения порядка, то есть избавиться от учитывания порядка. Число перестановок это

. Тогда будет
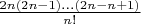
, или
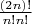
Проблема была только в том, что в пункте 6 я не учёл, что член из скобки не должен умножаться не только на себя, но и на противоположного из своей скобки.
Тогда в числителе, на каждую новую ячейку нужно выбрасывать на один элемент, а 2, ну и получается тогда конечное правильное выражение для числителя: