Задача. Доказать, что

равномерно непрерывна на

.
Я изначально решал так (и в учебнике такой же способ). Разобьем

на
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
и

. На первом промежутке функция равномерно непрерывна, потому что он компактный. На втором, для любого

существует

, такая, что для любых
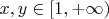
, если
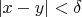
, то
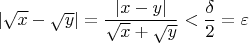
.
Объединяя результаты, получаем равномерную непрерывность на исходном промежутке.
Но потом нашел способ, кажется, гораздо проще. По крайней мере, не нужна теорема о равномерной непрерывности на компактном множестве, и не придется возиться с объединением. Для любого

существует
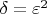
, такая, что для любых
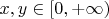
, если
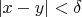
, то
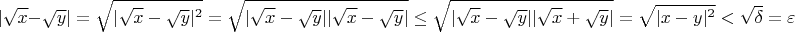
Все ли тут правильно? Если да, то странно, что его мало где приводят. В основном, везде решают первым способом.