Имел в виду просто множества, не ординалы. Верещагин, Шень
У них там и определение возведения в степень есть, страница 91 (в издании 2012 года). Да, возведение в степень ординалов определяется иначе, чем для множеств.
Тогда какому ординалу равно множество бесконечных последовательностей натуральных чисел
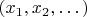
с лексикографическим порядком?
Никакому. Какой минимальный элемент в множестве последовательностей вида
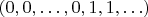
(конечное число нулей, потом единицы)?
И какой первый ординал имеет мощность континуума?

. Который определяется, как наименьший ординал мощностью континуум :)
Множество бесконечных последовательностей, в которых конечное число ненулевых элементов
Да, пардон, тут не написал - с обратным лексикографическим (т.е. сравниваем самые правые различающиеся элементы).