По работе возникли пара задачек, помогите разобраться, пожалуйста. Только сразу предупреждаю: я не физик-математик и даже не студент физики-математики, поэтому сильно не пытайте

. В этой теме выкладывают одну из них.
Есть цилиндр высоты

. На дне лежит шарик радиуса

. В начальный момент времени происходит две вещи.
1. Поршень начинает вдвигаться в цилиндр с постоянной скоростью

.
2. Шарик стартует со дна вертикально вверх с начальной скоростью

(предполагаем, что скорость достаточная для того, чтобы шарик поднялся на исходную высоту цилиндра).
На шарик действует гравитация с ускорением свободного падения

. Все столкновения абсолютно упругие. Вопрос: сколько соударений шарика с поршнем произойдет до того момента, когда поршень придавит шарик (то есть, поршень пройдет расстояние
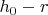
)?
Я решал итеративно, с помощью таблички в экселе. Время первой встречи шарика и поршня нашел решая квадратное уравнение из условия:
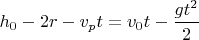
(см. рисунок). Обозначим это время за
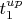
Затем, после удара, шарик за то же время упадет обратно. Обозначим общее время вверх-вниз
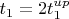
. В результате, через это время придем к начальной ситуации, когда шарик лежит внизу и начинает двигаться вверх, только теперь поршень находится не на высоте

, а на высоте
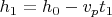
. Подставляя

вместо

в уравнение, находим момент времени
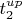
, и так далее.

Вопрос к знатокам следующий: можно ли как-то получить решение в замкнутом виде, чтобы не пересчитывать каждый раз кучу ячеек?