Расчет был на то, что люди будут доказывать его по индукции.
Никогда не задумывался, но тут взялся проверить (хотя наверняка не я первый), как выглядит последовательность
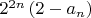
, где

- левая часть неравенства. Так вот она довольно быстро выходит на плато примерно на значении
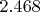
. Но длины мантиссы не хватает, чтобы проверить дальше

. Чудесато...